Difference between revisions of "BSc: IntroductionToCombinatoricsAndDiscreteMathematics"
V.matiukhin (talk | contribs) |
V.matiukhin (talk | contribs) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 380: | Line 380: | ||
* <math>F_0^2+F_1^2+\ldots+F_n^2</math>; |
* <math>F_0^2+F_1^2+\ldots+F_n^2</math>; |
||
| − | * <math>F_0^3+ |
+ | * <math>F_0^3+F_1^3+\ldots + F_n^3</math>. |
| Line 475: | Line 475: | ||
| − | + | Пусть <math>1= (1,0,0,\ldots,0,\ldots)</math>, <math>t = (0,1,0,\ldots,0,\ldots)</math>. |
|
| + | 1) Найдите <math>t^2, t^3, \ldots, t^n</math>. |
||
| − | |||
| − | |||
| − | 1) Найдите <math>t^2, t^3, \idots, t^n</math>. |
||
2) Покажите, что любая последовательность <math>(a_0,a_1,\ldots,a_n,\ldots,)</math> единственным образом представляется в виде <math>a_0 \cdot 1 + a_1 \cdot t + a_2 \cdot t^2 + \ldots + a_n \cdot t^n + \ldots</math>. |
2) Покажите, что любая последовательность <math>(a_0,a_1,\ldots,a_n,\ldots,)</math> единственным образом представляется в виде <math>a_0 \cdot 1 + a_1 \cdot t + a_2 \cdot t^2 + \ldots + a_n \cdot t^n + \ldots</math>. |
||
| Line 485: | Line 483: | ||
| − | + | Покажите, что все свойства многочленов (коммутативность по сложению/умножению, ассоциативность, дистрибутивность) переносятся на формальные степенные ряды. |
|
| − | 2) Пусть дан ряд <math>f(t)</math>. Корректна ли операция подстановки вместо <math>t</math> ряда <math>g(t)</math>? Ряда <math>g(t)</math> без свободного члена? |
||
| + | Пусть дан ряд <math>f(t)</math>. Корректна ли операция подстановки вместо <math>t</math> ряда <math>g(t)</math>? Ряда <math>g(t)</math> без свободного члена? |
||
| − | в) Определим ''производную'' формального степенного ряда <math>A = a_0 \cdot 1 + a_1 \cdot t + \ldots + a_n \cdot t^n + \ldots</math> как ряд <math>A' = a_1 + 2a_2 t + \ldots + n a_n t^{n-1} + \ldots</math>. Производную можно брать несколько раз подряд, через <math>A^{(n)}</math> обозначается <math>n</math>-ая производная ряда <math>A</math>. |
||
| + | Определим ''производную'' формального степенного ряда <math>A = a_0 \cdot 1 + a_1 \cdot t + \ldots + a_n \cdot t^n + \ldots</math> как ряд <math>A' = a_1 + 2a_2 t + \ldots + n a_n t^{n-1} + \ldots</math>. Производную можно брать несколько раз подряд, через <math>A^{(n)}</math> обозначается <math>n</math>-ая производная ряда <math>A</math>. |
||
| − | 1) Производная линейна, то есть <math>(\alpha A + \beta B)' = \alpha A' + \beta B'</math> (здесь <math>\alpha,\beta \in \R</math>, <math>A,B</math> --- формальные степенные ряды). |
||
| + | Производная линейна, то есть <math>(\alpha A + \beta B)' = \alpha A' + \beta B'</math> (здесь <math>\alpha,\beta \in \R</math>, <math>A,B</math> --- формальные степенные ряды). |
||
| − | 2) Выполнено ''тождество Лейбница'', то есть <math>(AB)' = A'B + AB'</math>. |
||
| + | Выполнено ''тождество Лейбница'', то есть <math>(AB)' = A'B + AB'</math>. |
||
| − | 3) (''Ряд Тейлора в нуле''). Докажите, что <math>a_n</math> --- свободный член ряда <math>\frac{A^{(n)}}{n!}</math>. |
||
| + | (''Ряд Тейлора в нуле''). Докажите, что <math>a_n</math> --- свободный член ряда <math>\frac{A^{(n)}}{n!}</math>. |
||
Пусть <math>F=1+t+t^2+\dots</math>, <math>G=1-t+t^2-t^3+\dots</math>. Найдите <math>F+G</math>, <math>F\cdot G</math>. |
Пусть <math>F=1+t+t^2+\dots</math>, <math>G=1-t+t^2-t^3+\dots</math>. Найдите <math>F+G</math>, <math>F\cdot G</math>. |
||
| − | |||
Пусть <math>F = \sum_{k=0}^{\infty} \frac{1}{k!}t^k</math>, <math>G = \sum_{k=0}^{\infty} \frac{(-1)^k}{k!}t^k</math>. Найдите <math>F \cdot G</math> и <math>F^2</math>. |
Пусть <math>F = \sum_{k=0}^{\infty} \frac{1}{k!}t^k</math>, <math>G = \sum_{k=0}^{\infty} \frac{(-1)^k}{k!}t^k</math>. Найдите <math>F \cdot G</math> и <math>F^2</math>. |
||
| − | |||
Существует ли два таких ненулевых степенных ряда <math>F,G</math>, что <math>F\cdot G = F+G</math>? |
Существует ли два таких ненулевых степенных ряда <math>F,G</math>, что <math>F\cdot G = F+G</math>? |
||
| + | Ряд <math>G</math> называется ''обратимым'', если существует такой ряд <math>F</math>, что <math>F\cdot G=1</math>. <math>F</math> называется ''рядом, обратным к <math>G</math>'' и обозначается так: <math>F = G^{-1}</math>. |
||
| − | Ряд <math>G</math> называется ''обратимым'', если существует такой ряд <math>F</math>, что <math>F\cdot G=1</math>. <math>F</math> называется ''рядом, обратным к <math>G</math>'' и обозначается так: <math>F = G^{-1}</math>. |
||
| Line 517: | Line 513: | ||
| − | Найдите коэффициенты ряда |
+ | Найдите коэффициенты ряда <math>\frac{1}{1-t}</math>; <math>\frac1{2-t}</math>; <math>\frac1{3+4t}</math>; <math>\frac1{(1-t)^{2}}</math>; <math>\frac1{(1-t)^{m}}</math>. |
| − | Верно ли равенство |
+ | Верно ли равенство <math>\left(\frac{1}{1-t}\right)^2 \cdot \left(\frac{1}{1+t}\right)^2 = \left(\frac{1}{1-t^2}\right)^2</math> для формальных степенных рядов? |
| Line 626: | Line 622: | ||
| style="width:25%" | Форма текущего контроля<br> |
| style="width:25%" | Форма текущего контроля<br> |
||
| style="width:50%" | Материалы текущего контроля<br> |
| style="width:50%" | Материалы текущего контроля<br> |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | 1 || Основные правила комбинаторики || Письменная контрольная || На кафедре дискретной математики лежит стопка 63 непроверенных контрольных работ студентов из четырёх разных групп: 20 работ из 312, 15 работ из 323, 18 работ из 324 и 10 работ из 325. Семинарист хочет взять наугад несколько работ на проверку. Какое минимальное количество работ необходимо взять, чтобы среди них гарантированно нашлось |
||
| + | |||
| + | а) 4 работы из одной группы; |
||
| + | |||
| + | б) 4 работы из 323 группы; |
||
| + | |||
| + | в) 2 работы из одной группы и 2 работы из другой группы; |
||
| + | |||
| + | г) по одной работе из каждой из четырёх групп? |
||
| + | |||
| + | '''В этой задаче каждый пункт оценивается в 1 балл.''' |
||
| + | |||
| + | |||
| + | |||
| + | 27 точек образуют прямоугольник размер <math>3 \times 9</math>. Каждая точка покрашена в красный или синий цвет. Докажите, что существуют 4 точки одного цвета, образующие одноцветный прямоугольник (со сторонами, параллельными исходному прямоугольнику). |
||
| + | |||
| + | |||
| + | При каком минимальном значении <math>m</math> для прямоугольника из <math>6 \times m</math> точек, покрашенных в пять цветов, гарантированно найдётся одноцветный прямоугольник? |
||
| + | |||
| + | [[Image:pic3dm1.png]] |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | 2 || Основные комбинаторные величины || Письменная контрольная || Даны множества <math>A,B</math>, причём <math>|A|=4</math>, <math>|B|=7</math>. Найдите количество таких соответствий <math>f: A \to B</math>, что: |
||
| + | а) <math>f^{-1}</math> --- сюръективное отображение; |
||
| + | б) <math>f^{-1}</math> --- сюръективное соответствие; |
||
| + | в) <math>f</math> --- инъективное соответствие; |
||
| + | г) <math>f</math> --- инъективное отображение. |
||
| + | '''В этой задаче каждый пункт оценивается в 2 балла. Ответ надо дать в виде суммы не более 10 слагаемых, без использования чисел сочетаний/размещений/полиномиальных коэффициентов''' |
||
| + | |||
| + | |||
| + | |||
| + | Имеется 4 коробки (красная, синяя, желтая, зеленая), и 9 шаров (3 красных, 2 синих, и по одному желтому, зеленому, фиолетовому и белому). Сколькими способами можно разложить шары по коробками, если нужно чтобы в каждой коробке что-то лежало? |
||
| + | ''Ответ дайте в виде суммы не более 10 слагаемых, '''без использования''' знаков вида <math>C_*^*</math>, <math>A_*^*</math>, <math>P(*,*,*)</math>'' |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | 3 || Тождества с биномиальными коэффициентами || Письменная контрольная || Напишите коэффициент у данного монома в данном разложении (Ответ надо дать в виде суммы не более 10 слагаемых, разрешается использовать символ <math>P(*,*,*)</math>): |
||
| + | |||
| + | а) <math>x^{25}</math> в <math>(x^2+x^4-x^7)^{10}</math>; |
||
| + | |||
| + | б) <math>x^{26}</math> в <math>(x^2+x^4-x^7)^{10}</math>; |
||
| + | |||
| + | в) <math>x^{27}</math> в <math>(x^2+x^4-x^7)^{10}</math>. |
||
| + | |||
| + | |||
| + | |||
| + | Докажите тождество: |
||
| + | <math>\sum_{k=r}^n C_n^k \cdot C_k^r \cdot 3^k = C_n^r \cdot 3^r \cdot 4^{n-r}</math> |
||
| + | |||
| + | |||
| + | 20 студентов (студенты разные) сдают экзамен в три дня. Студент может прийти в один из дней, а может и не прийти вовсе (неявка). Сколько существует различных распределений студентов по дням, таких чтобы |
||
| + | а) все студенты пришли на экзамен; |
||
| + | б) в первый день пришёл хотя бы один студент; |
||
| + | в) в каждый из дней пришли ровно 5 студентов? |
||
| + | Теперь предположим, что экзамен длится 7 дней, а каждый студент имеет несколько попыток. Сколько существует различных распределений студентов по дням, таких чтобы |
||
| + | г) каждый студент пришёл на экзамен трижды, причём в разные дни; |
||
| + | д) каждый студент пришёл на экзамен трижды, но теперь необязательно в разные дни? |
||
| + | '''В ответах разрешается использовать только знаки арифметических действий, возведение в степень, а также факториалы, <math>C_{\ast}^{\ast}</math>, <math>A_{\ast}^{\ast}</math> и <math>P(\ast,\ldots,\ast)</math>.''' |
||
| + | |||
| + | |||
| + | Хитрый пароль состоит из двух частей. Первая часть --- код из 4 цифр, в которых как минимум две чётные цифры. Вторая часть --- код из 7 различных цифр, из которых первые 4 идут по возрастанию, а оставшиеся 3 по убыванию. Сколько существует хитрых паролей? |
||
| + | ''Ответ разрешается оставить в виде суммы нескольких слагаемых (без троеточий) с использованием факториалов, <math>C_{\ast}^{\ast}</math>, <math>A_{\ast}^{\ast}</math> и <math>P(\ast,\ldots,\ast)</math>'' |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | 4 || Рекуррентные соотношения || Письменная контрольная || Имеется алфавит из 6-х символов <math>\{a,b,c,d,e,f\}</math>. Обозначим через <math>A_n</math> количество последовательностей длины <math>n</math>, которые содержат нечётное количество символов <math>a</math>. Найдите и решите рекуррентное соотношение для <math>A_n</math>. |
||
| + | |||
| + | |||
| + | |||
| + | В наличии имеются плитки размеров <math>1\times 1</math>, <math>1 \times 2</math> нескольких типов. Для каждого набора плиток |
||
| + | найдите рекуррентное соотношение для <math>a_n</math>, количества способов выложить плитку размером <math>1\times n</math> и выпишите явную формулу для решения |
||
| + | |||
| + | Заполните таблицу. |
||
| + | {| class="wikitable" |
||
| + | |- |
||
| + | ! набор плиток |
||
| + | ! рекуррентное соотношение 2-го порядка |
||
| + | ! явная формула |
||
| + | |- |
||
| + | | 1 вид плитки размера <math>1\times 1;</math> |
||
| + | | <math>a_{n+2} = a_{n+1} + a_n,\ a_1 = 1,\ a_2 = 2</math> |
||
| + | | <math>\frac{1+\sqrt{5}}{2\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n - \frac{1-\sqrt{5}}{2\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^n</math> |
||
| + | |- |
||
| + | | 1 вид плитки размера <math>1\times 2</math> |
||
| + | | |
||
| + | | |
||
| + | |- |
||
| + | | 2 вида плитки размера <math>1\times 1;</math> |
||
| + | | |
||
| + | | |
||
| + | |- |
||
| + | | 1 вид плитки размера 1 <math> \times 2</math> |
||
| + | | |
||
| + | | |
||
| + | |- |
||
| + | | 2 вида плитки размера <math>1\times 1;</math> |
||
| + | | |
||
| + | | |
||
| + | |- |
||
| + | | 3 вида плитки размера 1 <math>\times 2</math> |
||
| + | | |
||
| + | | |
||
| + | |- |
||
| + | |} |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | 5 || Разбиения || Письменная контрольная || Обозначим через <math>f(n;n_1,\ldots,n_k)</math> количество упорядоченных разбиений <math>n</math> на слагаемые <math>n_1,\ldots,n_k</math>, а через <math>F (n;n_1,\ldots,n_k)</math> количество неупорядоченных разбиений <math>n</math> на слагаемые <math>n_1,\ldots,n_k</math>. Найдите |
||
| + | |||
| + | а) <math>f(9;1,2,3,4,5,6,7,8,9)</math>; |
||
| + | |||
| + | б) <math>f(11;1,3,5,7,9)</math>; |
||
| + | |||
| + | в) <math>F(10;1,3,5,7,9)</math>. |
||
| + | |||
| + | |||
| + | |||
| + | ==== Задача (10) ==== |
||
| + | Пусть <math>B</math> есть число способов представить число <math>100</math> в виде суммы нескольких различных элементов множества <math>\{1, 2, 3,\ldots,100\}</math> и такого же числа различных элементов множества <math>\{0, 1, 2, \ldots,99\}</math>. [Например, есть представления <math>(1+2)+(0+97)</math>, <math>(1)+(99)</math>, <math>(1+2+3)+(2+4+88)</math>.] Сравните <math>B</math> и <math>p(100)</math>, последнее -- это количество неупорядоченных разбиений числа <math>100</math>. |
||
| + | |||
| + | |||
| + | |||
| + | Пусть <math>B</math> есть число способов представить число <math>100</math> в |
||
| + | виде суммы нескольких различных элементов множества <math>\{1, 2, 3,\ldots,100\}</math> |
||
| + | и такого же числа различных элементов множества <math>\{0, 1, 2, \ldots,99\}</math>. [Например, |
||
| + | есть представления <math>(1+2)+(0+97)</math>, <math>(1)+(99)</math>, <math>(1+2+3)+(2+4+88)</math>.] |
||
| + | Сравните <math>B</math> и <math>p(100)</math>, последнее --- это количество неупорядоченных разбиений числа <math>100</math>. |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | 6 || Формальные степенные ряды и производящие функции || Письменная контрольная || Вычислите производящую функцию для следующих последовательностей. Преобразуйте формальный степенной ряд к отношению многочленов. |
||
| + | {| class="wikitable" |
||
| + | |- |
||
| + | ! последовательность <math>a_n</math> |
||
| + | ! производящая функция |
||
| + | |- |
||
| + | | числа Фибоначчи <math>0,1,1,2,\ldots</math> |
||
| + | | <math>\frac{t}{1-t-t^2}</math> |
||
| + | |- |
||
| + | | количество положительных целых |
||
| + | решений <math>(a,b)</math> уравнения <math>a+b=n</math> |
||
| + | | |
||
| + | |- |
||
| + | | количество неотрицательных целых |
||
| + | решений <math>(a,b,c)</math> уравнения <math>a+b+c=n</math> |
||
| + | | |
||
| + | |- |
||
| + | | количество целых решений <math>(a,b,c)</math> |
||
| + | уравнения <math>a+b+c=n</math>, с условиями |
||
| + | <math>0\leq a \leq 6</math>, <math>0 \leq b \leq 3</math>, <math>0 \leq c \leq 1</math> |
||
| + | | |
||
| + | |} |
||
| + | |||
| + | |||
| + | |||
| + | Найдите радиус сходимости у следующих формальных степенных рядов. |
||
| + | |||
| + | а) <math>\frac{1}{1+4t}</math>; |
||
| + | |||
| + | б) <math>\frac{4}{1+9t}</math>; |
||
| + | |||
| + | в) <math>\frac{2t^2}{(1+9t^2)^2}</math>; |
||
| + | |||
| + | г) <math>\frac{1}{(t-2023)^{2023}}</math>; |
||
| + | |||
| + | д) <math>\frac{1}{\sqrt{1-3t}}</math>. |
||
| + | |||
| + | |||
| + | |||
| + | Найдите коэффициент при <math>x^{2023}</math> у следующих формальных степенных рядов. |
||
| + | |||
| + | а) <math>\frac{1}{1+4t}</math>; |
||
| + | |||
| + | б) <math>\frac{4}{1+9t}</math>; |
||
| + | |||
| + | в) <math>\frac{2t^2}{(1+9t^2)^2}</math>; |
||
| + | |||
| + | г) <math>\frac{1}{(t-2023)^{2023}}</math>; |
||
| + | |||
| + | д) <math>\frac{1}{\sqrt{1-3t}}</math>. |
||
| + | |||
|} |
|} |
||
| Line 639: | Line 808: | ||
'''Вопросы/Задания к промежуточной аттестации в устной/письменной форме:''' |
'''Вопросы/Задания к промежуточной аттестации в устной/письменной форме:''' |
||
| + | |||
| − | 1.<br>2.<br>3.<br>...<br>48.<br>49.<br>50.<br>... |
||
| + | 1. Правило сложения. Правило умножения. Примеры: автомобильные номера, количество шестизначных чисел с различными условиями на цифры (задача 7.3). Принцип Дирихле. Пример на принцип Дирихле с квадратом. |
||
| + | |||
| + | 2. Размещения, перестановки и сочетания. Доказательство формул для чисел размещения и сочетания с повторениями и без повторений. Типовые задачи (аналогичные 7.5, 7.6, 7.7, 7.8). |
||
| + | |||
| + | 3. Бином Ньютона. Полиномиальный коэффициент и полиномиальная формула. Типовые задачи (аналогичные задачам 7.10, 8.5). |
||
| + | |||
| + | 4. Комбинаторные тождества (6 штук). |
||
| + | |||
| + | 5. Формула включений и исключений (формулировка и док-во для <math>n=3</math>). Формула для количества беспорядков на <math>n</math> элементах (Задача 9.4 про перестановки книг). |
||
| + | |||
| + | 6. Формула включений и исключений (формулировка и док-во для <math>n=3</math>). Формула для количества сюръекций из <math>k</math>-элементного множества в <math>m</math>-элементное (Задача 9.5 про домики). |
||
| + | |||
| + | 7. Задачи о разбиениях чисел на слагаемые. Упорядоченные и неупорядоченные разбиения. Рекуррентные формулы. (Задача 12.2 а)б)). |
||
| + | |||
| + | 8. Задачи о разбиениях чисел на слагаемые. Упорядоченные разбиения. Количество всех упорядоченных разбиений на произвольные слагаемые. (Задача 12.1 а)б)). |
||
| + | |||
| + | 9. Диаграммы Юнга. Теоремы Эйлера о равенстве количеств неупорядоченных разбиений числа <math>n</math> на <math>k</math> или не более, чем <math>k</math> слагаемых (3 штуки). |
||
| + | |||
| + | 10. Линейные рекуррентные соотношения с постоянными коэффициентами. Характеристическое уравнение. Общая формула для соотношения <math>n</math>-го порядка (формулировка, частный случай <math>n=2</math> --- б/д). Формула для чисел Фибоначчи. |
||
| + | |||
| + | 11. Формальные степенные ряды, операции над ними. Пример вычисления суммы и произведения (Задача 14.3). |
||
| + | |||
| + | 12. Формальные степенные ряды. Определение обратного ряда. Пример деления в столбик. Примеры нахождения обратных рядов (задача 14.6). |
||
| + | |||
| + | 13. Числа Фибоначчи и их производящая функция. Радиус сходимости, значение <math>\sum_{n=0}^{\infty} \frac{F_n}{2^n}</math>. |
||
| + | |||
| + | 14. Числа Каталана. Производящая функция для чисел Каталана. |
||
| + | |||
| + | 15. Задача о раскраске множества в два цвета. |
||
| + | |||
| + | 16. Сумма степеней натуральных чисел. |
||
| + | |||
| + | 17. Знакопеременные тождества (2 штуки): сумма биномиальных коэффициентов и количество сюръекций. |
||
| + | |||
| + | 18. Формула включений и исключений. |
||
| + | |||
| + | 19. Формула включений и исключений (формулировка и док-во для <math>n=3</math>). Формула для функции Эйлера через произведение по простым сомножителям (док-во через формулу вкл-искл.) (Задача 9.1в.) |
||
| + | |||
| + | 20. Формула обращения Мёбиуса. |
||
| + | |||
| + | 21. Функция Эйлера. Формула с произведением по простым числам: доказательство при помощи формулы обращения Мёбиуса (Задача 10.6в). |
||
| + | |||
| + | 22. Линейные рекуррентные соотношения с постоянными коэффициентами. Характеристическое уравнение. Общая формула для соотношения 2-го порядка с одинаковыми корнями характеристического уравнения. |
||
| + | |||
| + | 23. Линейные рекуррентные соотношения с постоянными коэффициентами. Характеристическое уравнение. Общая формула для соотношения 2-го порядка с различными корнями характеристического уравнения. |
||
| + | |||
| + | 24. Формальный степенной ряд <math>(1-x)(1-x^2)(1-x^3)\ldots</math>. Теорема Эйлера о коэффициентах этого ряда (формулировка). Проверка верности теоремы Эйлера для <math>k=1,2</math>. Теорема о количестве разбиений на чётное и нечётное количество различных слагаемых (формулировка). |
||
| + | |||
| + | 25. Формальные степенные ряды. Строгое формальное определение через последовательности. Пример вычисления суммы и произведения рядов (Задача 14.3) |
||
| + | |||
| + | 26. Формальные степенные ряды, операции над ними. Определение обратного ряда. |
||
| + | Пример деления в столбик. Комбинаторное тождество, получаемое с использованием формального степенного ряда <math>\frac{1}{(1-x^2)^2}</math>. |
||
| + | |||
| + | 27. Формальные степенные ряды, операции над ними. Определение обратного ряда. Критерий обратимости ряда (задача 14.5). |
||
| + | |||
| + | 28. Вычисление суммы <math>\sum_{k=0}^n k^2 C_n^k \left(\frac{1}{17}\right)^k</math>. |
||
| + | |||
| + | 29. Определение радиуса сходимости формального степенного ряда. Теорема Коши-Адамара о сходимости степенных рядов (формулировка). Примеры, иллюстрирующие теорему (3 примера, показывающие, что на границе может быть сходимость/расходимость, задача 15.2). |
||
| + | |||
| + | 30. Принцип Дирихле. Оценки мощности множества попарно неортогональных <math>(-1,0,1)</math>-векторов: верхняя оценка величиной 140 и нижняя оценка величиной 70. |
||
| + | |||
| + | 31. Числа Каталана. Формула для коэффициентов ряда <math>\sqrt{1+x}</math>. (Задача 14.9) |
||
| + | |||
| + | 32. Числа Каталана. Формула для коэффициентов ряда <math>\sqrt{1+x}</math> (б/д). Вывод из неё формулы для чисел Каталана. |
||
| + | |||
| + | 33. Производящая функция для количества неупорядоченных разбиений в общем виде и для разбиений специального вида (задача 15.10). Доказательство того, что количества разбиений на попарно различные слагаемые и на нечётные слагаемые совпадают. |
||
| + | |||
| + | |||
=== Перечень учебно-методического обеспечения дисциплины === |
=== Перечень учебно-методического обеспечения дисциплины === |
||
| Line 653: | Line 890: | ||
| style="width:20%" | Вид учебных<br>занятий/деятельности |
| style="width:20%" | Вид учебных<br>занятий/деятельности |
||
| style="width:80%" | Деятельность обучающегося |
| style="width:80%" | Деятельность обучающегося |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| − | |- |
||
| + | | style="text-align:center;" | Лекция || Написание конспекта лекций: кратко, схематично, последовательно фиксировать основные положения лекции, выводы, формулировки, обобщения; помечать важные мысли, выделять ключевые слова, термины. Обозначить вопросы, термины или другой материал, который вызывает трудности, пометить и попытаться найти ответ в рекомендуемой литературе. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия. |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | Практическое (семинарское) занятие || При подготовке к семинарскому (практическому) занятию необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме. На основании обработанной информации постараться сформировать собственное мнение по выносимой на обсуждение тематике. Обосновать его аргументами, сформировать список источников, подкрепляющих его. |
||
| + | Во время семинарского (практического) занятия активно участвовать в обсуждении вопросов, высказывать аргументированную точку зрения на проблемные вопросы. Приводить примеры из источниковой базы и научной и/или исследовательской литературы. |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | Устный/письменный опрос || Отвечать, максимально полно, логично и структурировано, на поставленный вопрос. Основная цель – показать всю глубину знаний по конкретной теме или ее части. |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | Контрольная работа || При подготовке к контрольной работе необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. |
||
| + | |||
|} |
|} |
||
=== Методы и технологии обучения, способствующие формированию компетенции === |
=== Методы и технологии обучения, способствующие формированию компетенции === |
||
| Line 660: | Line 906: | ||
| Методы и технологии обучения, способствующие формированию компетенции |
| Методы и технологии обучения, способствующие формированию компетенции |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| + | | Информационно – коммуникационная технология, Педагогика сотрудничества, Традиционные технологии, Модульная технология |
||
| − | | |
||
|} |
|} |
||
Latest revision as of 01:09, 4 April 2024
Введение в комбинаторику и дискретную математику
- Квалификация выпускника: бакалавр
- Направление подготовки: 09.03.01 - “Информатика и вычислительная техника”
- Направленность (профиль) образовательной программы: Математические основы ИИ
- Программу разработал(а):
1. Краткая характеристика дисциплины
Изучение дисциплины обеспечивает формирование и развитие компетенций обучающихся в области комбинаторики и дискретной математики, их применение для решения различных прикладных задач в рамках профессиональной деятельности. В ходе освоения дисциплины обучающиеся рассматривают основные правила комбинаторики (сложение, умножение, принцип Дирихле, формула включений и исключений), концепции (числа сочетаний и размещений, рекуррентные соотношения, разбиения, формальные степенные ряды и производящие функции).
2. Перечень планируемых результатов обучения
- Целью освоения дисциплины
- Задачами дисциплины являются изучение основных правил и концепций комбинаторики для различных прикладных задач.
Общая характеристика результата обучения по дисциплине
- Знания: сформированы систематические знания по комбинаторике и дискретной математики.
- Умения:
- Навыки (владения):
3. Структура и содержание дисциплины
| № п/п |
Наименование раздела дисциплины |
Содержание дисциплины по темам |
| 1. | Основные правила комбинаторики | - правило сложения
- правило умножения - правило дополнения - принцип Дирихле |
| 2. | Основные комбинаторные величины | - размещения с повторениями / без повторений
- сочетания с повторениями/ без повторений - перестановки - треугольник Паскаля - линейный город - биномиальный и полиномиальный коэффициент |
| 3. | Тождества с биномиальными коэффициентами | - симметричность
- унимодальность - рекуррентное соотношение - Бином Ньютона - сумма биномиальных коэффициентов (в том числе альтернированная) - сумма квадратов биномиальных коэффициентов - сумма степеней натуральных чисел - формула включений и исключений - число беспорядков |
| 4. | Рекуррентные соотношения | - линейные однородные рекуррентные соотношения
- л.о.р.с. для степени 2 с разными корнями - л.о.р.с. для степени 2 с кратным корнем - формулировка теоремы в общем случае - числа Фибоначчи - формулировка теоремы для неоднородного случая |
| 5. | Разбиения | - упорядоченные и неупорядоченные разбиения
- диаграммы Юнга - теоремы Эйлера о равенстве неупорядоченных разбиений - асимптотика неупорядоченных разбиений |
| 6 | Формальные степенные ряды и производящие функции | - формальные степенные ряды
- обратимость ряда, пример деления в столбик - доказательство комб. тождеств при помощи формального степенного ряда - производящие функции для рекуррентных соотношений - возведение ряда в степень - числа Каталана |
4. Методические и оценочные материалы
Задания для практических занятий:
| № п/п |
Наименование раздела дисциплины (модуля) |
Перечень рассматриваемых тем (вопросов) |
| 1 | Основные правила комбинаторики | Принцип Дирихле. Пусть есть ящиков и кроликов. Если расселить кроликов по ящикам, то найдется хотя бы один ящик, в котором окажутся не менее кроликов.
В мешке имеется красных шара, зеленых шаров, синих, желтых и по белых, черных и серых (всего шаров). Сколько шаров необходимо вынуть из мешка, чтобы среди них гарантированно нашлось шаров одного цвета?
Комиссия из человек провела заседаний, причем на каждом заседании присутствовали ровно членов комиссии. Докажите, что найдутся два члена комиссии, по крайней мере дважды встречавшиеся на заседаниях.
В таблице расставлены целые числа, причем любые два числа в соседних клетках отличаются не более, чем на . Докажите, что среди этих чисел найдутся два равных.
Пусть имеется множество из слов в алфавите из символа. Докажите, что хотя бы одно из слов не короче .
В правильном треугольнике со стороной отмечено пять точек. Докажите, что найдется пара точек, удаленных друг от друга не более, чем на . |
| 2 | Основные комбинаторные величины | Пусть . Извлекать элементы из можно по порядку или <<пригорошнями>>. Первые называются размещениями, вторые --- сочетаниями. При этом каждое из них бывает как с повторениями символов, так и без.
Размещение с повторениями --- это снова любой набор объектов , расположенных друг за другом в определенном порядке. Только теперь объекты в размещении могут совпадать. Например, «жаба» и «абаж» --- два разных 4-размещения с повторениями из букв русского алфавита. Сочетания без повторений отличаются от размещений без повторений тем, что в них порядок объектов значения не имеет. Так, «лягушка» и «гуляшка» представляют собой одно и то же 7-сочетание без повторений букв {л, я, г, у, ш, к, а } русского алфавита. Сочетания с повторениями аналогично, например { ж, а, б, а } = { а, б, а, ж }.
Сформулируйте на языке теории множеств что такое размещение с повторениями/ без повторений и сочетания с повторениями (не используя понятий набор и порядок, разрешается использовать все определения из первых двух листков, например: множество, элемент, подмножество, все виды отображений, декартово произведение). Докажите формулу для числа размещений без повторений (если вы будете пользоваться правилом умножения, сформулируйте чётко, какие множества A и B вы используете).
(а) Сколько существует шестизначных чисел? (б) Сколько существует шестизначных чисел, делящихся на 5? (в) Сколько существует шестизначных чисел, в записи которых присутствует хотя бы одна чётная цифра?
На плоскости отмечено 10 точек так, что никакие три из них не лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках?
балбесов-первокурсников и семинарист пришли в кинотеатр и сели в одном ряду. Семинарист должен сидеть с краю, а Петю, Колю и Васю нельзя сажать втроем. Сколькими способами можно рассадить группу?
Из класса, в котором учатся человек, назначаются на дежурство в столовую человека. Сколькими способами это можно сделать? Сколько существует способов набрать команду дежурных, в которую попадет ученик этого класса Коля Васин? В группе учатся студентов. Согласно новому указу Минздрава группы нужно вакцинировать. Сколькими способами это можно сделать? Выяснилось, что один студент этой группы Коля Васин уже провакцинирован. Сколько теперь существует способов исполнить указ Минздрава?
У королевы есть одинаковых зеркал. Сколькими способами их можно повесить в разных залах замка так, чтобы в каждом зале было хотя бы одно зеркало?
В пекарне продавались вида пирожков: элеши, эчпочмаки, перемячи и кыстыбыи. Сколькими способами можно купить пирожков?
Есть попарно различных чашек и неразличимых стаканов. Также имеется попарно различных ложек и неразличимых кусков сахара. Сколькими способами можно разложить: а) ложки по чашкам; б) сахар по чашкам; в) ложки по стаканам, если ?
На ютуб-канале есть плейлист из лекций по ДМ. Сколькими способами их можно переставить так, чтобы а) шесть лекций, прочитанных Даниилом Владимировичем, расположились в правильном порядке (но не обязательно подряд)? б) те же лекции по-прежнему были в правильном порядке, но никакие в) две из них не шли подряд?
Сколько имеется способов раздать разных цветков, трём девушкам: какой-то --- , а остальным~--- по цветка?
Дано множество . Даны числа , .
Сколькими способами можно выбрать из полной колоды, содержащей карты, карт так, чтобы среди них были все масти? |
| 3 | Тождества с биномиальными коэффициентами | Покажите, что число -сочетаний без повторений из -элементного множества равно
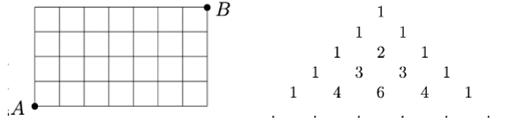
а) Количеству последовательностей из 0 и 1 длины с ровно единицами. б) (Линейный город) Количеству маршрутов путей из в , если идти можно только вправо и вверх (стороны прямоугольника и ) в) (Треугольник Паскаля) -ому числу в -ой строке треугольника Паскаля (нумерация с ) г) (Бином Ньютона) Коэффициенту при мономе в разложении .
- через непосредственное определение - при помощи формулы - используя интерпретации выше Докажите следующие тождества при целых неотрицательных: а) б) в)
Найдите суммы при целых неотрицательных : а) б) в) г*) д) е) ж) з) и) к) л) м*) н*)
Найдите . Посчитайте коэффициенты при и в разложении .
В комнате площади уложены три ковра площади каждый (форма комнаты и ковров произвольная). Докажите, что какие-то два из этих трёх ковров перекрываются по площади, не меньшей~.
|
| 4 | Рекуррентные соотношения | Для каждого из следующих линейных рекуррентных соотношений найдите общее решение:
а) б) ; в) г) д) е) .
Найдите решение неоднородного линейного рекуррентного соотношения а) ; б) ; в) ?
Числами Фибоначчи называется последовательность , удовлетворяющая соотношениям , , для всех натуральных .
Найдите формулу для нахождения -ого члена последовательности .
Найдите
Сколькими способами можно разменять купюру в рублей на монеты достоинством , и рублей? %364
Найдите рекуррентное соотношение для последовательности , где -- число способов выложить прямоугольник размера
Сколько существует строк из нулей и единиц, в каждой из которых никакие два нуля не стоят рядом?
Докажите, что последовательность с общим членом удовлетворяет соотношению .
В центральной клетке левого столбца доски 1000 × 3 стоит шахматный король. Сколькими спо[1]собами он может добраться до правого столбца доски за 999 ходов? |
| 5 | Разбиения | а) Найдите количество упорядоченных разбиений числа на слагаемых.
б) Найдите общее количество упорядоченных разбиений числа на слагаемые. в) Какой ответ будет в предыдущих пунктах, если мы разрешим слагаемым принимать значение ?
Обозначим через () количество упорядоченных (соотв. неупорядоченных) разбиений на слагаемые .
Справедливы следующие рекуррентные формулы а) ; б) . в) Каковы начальные условия в этих формулах?
а) Что больше: или ? б) Найдите оба числа, используя рекуррентные формулы.
Диаграмма Юнга -- это конечный набор клеток, выровненных по левой границе, в котором длины строк образуют невозрастающую последовательность (каждая строка такой же длины как предыдущая, или короче). Весом диаграммы Юнга называется общее количество клеток диаграммы. Набор чисел, состоящий из длин строк, задаёт разбиение веса диаграммы в сумму слагаемых. Таким образом, есть соответствие между всеми неупорядоченными разбиениями натурального числа и всеми диаграммами Юнга веса .
Сколько существует диаграмм Юнга произвольного веса, но имеющих не более строк и не более столбцов?
На доске написано несколько целых положительных чисел: , , , , . Пишем на другой доске следующие числа: --- сколько всего чисел на первой доске, --- сколько там чисел, больших единицы, --- сколько там чисел, больших двойки, и т.~д., пока получаются положительные числа. На этом заканчиваем --- нули не пишем. На третьей доске пишем числа , , , , построенные по числам второй доски аналогичным образом. Докажите, что наборы чисел на первой и третьей досках совпадают.
|
| 6 | Формальные степенные ряды и производящие функции | Рассмотрим множество последовательностей (здесь берутся из множества чисел , или ) и введём на них операции сложения и умножения следующим образом:
Пусть , . 1) Найдите . 2) Покажите, что любая последовательность единственным образом представляется в виде .
Покажите, что все свойства многочленов (коммутативность по сложению/умножению, ассоциативность, дистрибутивность) переносятся на формальные степенные ряды.
Пусть дан ряд . Корректна ли операция подстановки вместо ряда ? Ряда без свободного члена?
Определим производную формального степенного ряда как ряд . Производную можно брать несколько раз подряд, через обозначается -ая производная ряда . Производная линейна, то есть (здесь , --- формальные степенные ряды). Выполнено тождество Лейбница, то есть . (Ряд Тейлора в нуле). Докажите, что --- свободный член ряда . Пусть , . Найдите , . Пусть , . Найдите и . Существует ли два таких ненулевых степенных ряда , что ? Ряд называется обратимым, если существует такой ряд , что . называется рядом, обратным к и обозначается так: .
Докажите, что ряд обратим тогда и только тогда, когда , причём обратный ряд единственен.
Найдите коэффициенты ряда ; ; ; ; .
Верно ли равенство для формальных степенных рядов?
Сформулируйте комбинаторное тождество, получаемое при приравнивании коэффициентов в этих рядах.
При каких условиях на степенной ряд его можно разделить на степенной ряд (то есть уравнение разрешимо относительно неизвестного степенного ряда )?
При каких условиях на степенной ряд разрешимо уравнение ?
Пусть ---- степенной ряд, задаваемый уравнением . Найдите коэффициенты .
Пусть . Положим .
Если , то совпадает с биномиальным коэффициентом.
Определим ряд . Покажите, что при определения согласованы.
Покажите, что .
Используя определение, найдите коэффициенты ряда . Сравните ответ с ответом в задаче предыдущей задаче пункте в.
Вычислите .
Найдите производящую функцию для числа
Докажите, что функции в последних двух пунктах совпадают.
, , , .
Приведите пример, когда на границе ряда (то есть при ) есть сходимость в обеих точках; расходимость в обеих точках; сходимость в одной точке и расходимость в другой точке.
Найдите производящую функцию для последовательности . \pu Какой у неё радиус сходимости?
В каких точках действительной прямой сходится ряд , где задано следующим образом?
|
Текущий контроль успеваемости обучающихся по дисциплине:
| № п/п |
Наименование раздела дисциплины |
Форма текущего контроля |
Материалы текущего контроля | |||||||||||||||||||||
| 1 | Основные правила комбинаторики | Письменная контрольная | На кафедре дискретной математики лежит стопка 63 непроверенных контрольных работ студентов из четырёх разных групп: 20 работ из 312, 15 работ из 323, 18 работ из 324 и 10 работ из 325. Семинарист хочет взять наугад несколько работ на проверку. Какое минимальное количество работ необходимо взять, чтобы среди них гарантированно нашлось
а) 4 работы из одной группы; б) 4 работы из 323 группы; в) 2 работы из одной группы и 2 работы из другой группы; г) по одной работе из каждой из четырёх групп? В этой задаче каждый пункт оценивается в 1 балл.
27 точек образуют прямоугольник размер . Каждая точка покрашена в красный или синий цвет. Докажите, что существуют 4 точки одного цвета, образующие одноцветный прямоугольник (со сторонами, параллельными исходному прямоугольнику).
| |||||||||||||||||||||
| 2 | Основные комбинаторные величины | Письменная контрольная | Даны множества , причём , . Найдите количество таких соответствий , что:
а) --- сюръективное отображение; б) --- сюръективное соответствие; в) --- инъективное соответствие; г) --- инъективное отображение. В этой задаче каждый пункт оценивается в 2 балла. Ответ надо дать в виде суммы не более 10 слагаемых, без использования чисел сочетаний/размещений/полиномиальных коэффициентов
Имеется 4 коробки (красная, синяя, желтая, зеленая), и 9 шаров (3 красных, 2 синих, и по одному желтому, зеленому, фиолетовому и белому). Сколькими способами можно разложить шары по коробками, если нужно чтобы в каждой коробке что-то лежало? Ответ дайте в виде суммы не более 10 слагаемых, без использования знаков вида , , | |||||||||||||||||||||
| 3 | Тождества с биномиальными коэффициентами | Письменная контрольная | Напишите коэффициент у данного монома в данном разложении (Ответ надо дать в виде суммы не более 10 слагаемых, разрешается использовать символ ):
а) в ; б) в ; в) в .
Докажите тождество:
| |||||||||||||||||||||
| 4 | Рекуррентные соотношения | Письменная контрольная | Имеется алфавит из 6-х символов . Обозначим через количество последовательностей длины , которые содержат нечётное количество символов . Найдите и решите рекуррентное соотношение для .
В наличии имеются плитки размеров , нескольких типов. Для каждого набора плиток найдите рекуррентное соотношение для , количества способов выложить плитку размером и выпишите явную формулу для решения Заполните таблицу.
| |||||||||||||||||||||
| 5 | Разбиения | Письменная контрольная | Обозначим через количество упорядоченных разбиений на слагаемые , а через количество неупорядоченных разбиений на слагаемые . Найдите
а) ; б) ; в) .
Задача (10)Пусть есть число способов представить число в виде суммы нескольких различных элементов множества и такого же числа различных элементов множества . [Например, есть представления , , .] Сравните и , последнее -- это количество неупорядоченных разбиений числа .
Пусть есть число способов представить число в виде суммы нескольких различных элементов множества и такого же числа различных элементов множества . [Например, есть представления , , .] Сравните и , последнее --- это количество неупорядоченных разбиений числа . | |||||||||||||||||||||
| 6 | Формальные степенные ряды и производящие функции | Письменная контрольная | Вычислите производящую функцию для следующих последовательностей. Преобразуйте формальный степенной ряд к отношению многочленов.
Найдите радиус сходимости у следующих формальных степенных рядов. а) ; б) ; в) ; г) ; д) .
Найдите коэффициент при у следующих формальных степенных рядов. а) ; б) ; в) ; г) ; д) .
|
Контрольные вопросы для подготовки к промежуточной аттестации:
| № п/п |
Наименование раздела дисциплины |
Вопросы |
Вопросы/Задания к промежуточной аттестации в устной/письменной форме:
1. Правило сложения. Правило умножения. Примеры: автомобильные номера, количество шестизначных чисел с различными условиями на цифры (задача 7.3). Принцип Дирихле. Пример на принцип Дирихле с квадратом.
2. Размещения, перестановки и сочетания. Доказательство формул для чисел размещения и сочетания с повторениями и без повторений. Типовые задачи (аналогичные 7.5, 7.6, 7.7, 7.8).
3. Бином Ньютона. Полиномиальный коэффициент и полиномиальная формула. Типовые задачи (аналогичные задачам 7.10, 8.5).
4. Комбинаторные тождества (6 штук).
5. Формула включений и исключений (формулировка и док-во для ). Формула для количества беспорядков на элементах (Задача 9.4 про перестановки книг).
6. Формула включений и исключений (формулировка и док-во для ). Формула для количества сюръекций из -элементного множества в -элементное (Задача 9.5 про домики).
7. Задачи о разбиениях чисел на слагаемые. Упорядоченные и неупорядоченные разбиения. Рекуррентные формулы. (Задача 12.2 а)б)).
8. Задачи о разбиениях чисел на слагаемые. Упорядоченные разбиения. Количество всех упорядоченных разбиений на произвольные слагаемые. (Задача 12.1 а)б)).
9. Диаграммы Юнга. Теоремы Эйлера о равенстве количеств неупорядоченных разбиений числа на или не более, чем слагаемых (3 штуки).
10. Линейные рекуррентные соотношения с постоянными коэффициентами. Характеристическое уравнение. Общая формула для соотношения -го порядка (формулировка, частный случай --- б/д). Формула для чисел Фибоначчи.
11. Формальные степенные ряды, операции над ними. Пример вычисления суммы и произведения (Задача 14.3).
12. Формальные степенные ряды. Определение обратного ряда. Пример деления в столбик. Примеры нахождения обратных рядов (задача 14.6).
13. Числа Фибоначчи и их производящая функция. Радиус сходимости, значение .
14. Числа Каталана. Производящая функция для чисел Каталана.
15. Задача о раскраске множества в два цвета.
16. Сумма степеней натуральных чисел.
17. Знакопеременные тождества (2 штуки): сумма биномиальных коэффициентов и количество сюръекций.
18. Формула включений и исключений.
19. Формула включений и исключений (формулировка и док-во для ). Формула для функции Эйлера через произведение по простым сомножителям (док-во через формулу вкл-искл.) (Задача 9.1в.)
20. Формула обращения Мёбиуса.
21. Функция Эйлера. Формула с произведением по простым числам: доказательство при помощи формулы обращения Мёбиуса (Задача 10.6в).
22. Линейные рекуррентные соотношения с постоянными коэффициентами. Характеристическое уравнение. Общая формула для соотношения 2-го порядка с одинаковыми корнями характеристического уравнения.
23. Линейные рекуррентные соотношения с постоянными коэффициентами. Характеристическое уравнение. Общая формула для соотношения 2-го порядка с различными корнями характеристического уравнения.
24. Формальный степенной ряд . Теорема Эйлера о коэффициентах этого ряда (формулировка). Проверка верности теоремы Эйлера для . Теорема о количестве разбиений на чётное и нечётное количество различных слагаемых (формулировка).
25. Формальные степенные ряды. Строгое формальное определение через последовательности. Пример вычисления суммы и произведения рядов (Задача 14.3)
26. Формальные степенные ряды, операции над ними. Определение обратного ряда. Пример деления в столбик. Комбинаторное тождество, получаемое с использованием формального степенного ряда .
27. Формальные степенные ряды, операции над ними. Определение обратного ряда. Критерий обратимости ряда (задача 14.5).
28. Вычисление суммы .
29. Определение радиуса сходимости формального степенного ряда. Теорема Коши-Адамара о сходимости степенных рядов (формулировка). Примеры, иллюстрирующие теорему (3 примера, показывающие, что на границе может быть сходимость/расходимость, задача 15.2).
30. Принцип Дирихле. Оценки мощности множества попарно неортогональных -векторов: верхняя оценка величиной 140 и нижняя оценка величиной 70.
31. Числа Каталана. Формула для коэффициентов ряда . (Задача 14.9)
32. Числа Каталана. Формула для коэффициентов ряда (б/д). Вывод из неё формулы для чисел Каталана.
33. Производящая функция для количества неупорядоченных разбиений в общем виде и для разбиений специального вида (задача 15.10). Доказательство того, что количества разбиений на попарно различные слагаемые и на нечётные слагаемые совпадают.
Перечень учебно-методического обеспечения дисциплины
Список основной литературы:
Список дополнительной литературы:
Методические указания для обучающихся по освоению дисциплины
| Вид учебных занятий/деятельности |
Деятельность обучающегося |
| Лекция | Написание конспекта лекций: кратко, схематично, последовательно фиксировать основные положения лекции, выводы, формулировки, обобщения; помечать важные мысли, выделять ключевые слова, термины. Обозначить вопросы, термины или другой материал, который вызывает трудности, пометить и попытаться найти ответ в рекомендуемой литературе. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия. |
| Практическое (семинарское) занятие | При подготовке к семинарскому (практическому) занятию необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме. На основании обработанной информации постараться сформировать собственное мнение по выносимой на обсуждение тематике. Обосновать его аргументами, сформировать список источников, подкрепляющих его.
Во время семинарского (практического) занятия активно участвовать в обсуждении вопросов, высказывать аргументированную точку зрения на проблемные вопросы. Приводить примеры из источниковой базы и научной и/или исследовательской литературы. |
| Устный/письменный опрос | Отвечать, максимально полно, логично и структурировано, на поставленный вопрос. Основная цель – показать всю глубину знаний по конкретной теме или ее части. |
| Контрольная работа | При подготовке к контрольной работе необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. |
Методы и технологии обучения, способствующие формированию компетенции
| Методы и технологии обучения, способствующие формированию компетенции |
| Информационно – коммуникационная технология, Педагогика сотрудничества, Традиционные технологии, Модульная технология |