Difference between revisions of "BSc: DifferentialAndPartialDifferentialEquations"
V.matiukhin (talk | contribs) |
V.matiukhin (talk | contribs) |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 55: | Line 55: | ||
| style="text-align:center;" | Тема 11. || Специальные типы систем ОДУ. || Теория Флоке. Матрица монодромии и мультипликаторы. Анализ устойчивости для решений уравнений с периодическими коэффициентами. Гамильтоновы системы. Сохранение гамильтониана. Сохранение фазового объема. Примеры. Принцип наименьшего действия. <br> |
| style="text-align:center;" | Тема 11. || Специальные типы систем ОДУ. || Теория Флоке. Матрица монодромии и мультипликаторы. Анализ устойчивости для решений уравнений с периодическими коэффициентами. Гамильтоновы системы. Сохранение гамильтониана. Сохранение фазового объема. Примеры. Принцип наименьшего действия. <br> |
||
|- style="background-color:#F8F9FA; color:#202122;" |
|- style="background-color:#F8F9FA; color:#202122;" |
||
| − | | style="text-align:center;" | Тема 12. || Сингулярные возмущения и релаксационные колебания. || Системы вида <math>\varepsilon |
+ | | style="text-align:center;" | Тема 12. || Сингулярные возмущения и релаксационные колебания. || Системы вида <math>\varepsilon d_t\overrightarrow{X}^\varepsilon = \vec{g}(\vec{X}^\varepsilon, \vec{Y}^\varepsilon, \varepsilon)</math>, <math>d_t\overrightarrow{Y}^\varepsilon = \vec{f}(\vec{X}^\varepsilon, \vec{Y}^\varepsilon, \varepsilon)</math>, где <math>0 < \varepsilon \ll 1</math>.Поверхность вырождения: устойчивые и неустойчивые участки. Фазовый портрет. Чередование быстрых и медленных движений. Периодические режимы. Уравнение Ван дер Поля. <br> |
|- style="background-color:#F8F9FA; color:#202122;" |
|- style="background-color:#F8F9FA; color:#202122;" |
||
| style="text-align:center;" | Тема 13. || Конечно-разностные уравнения и системы. || Формула Тейлора. Интерполяционный полином Лагранжа. Численная производная двухточечная и четырехточечная формулы для численной производной. Численное интегрирование. Оценки погрешностей численной производной и интеграла. Определение неподвижной точки. Теорема о неподвижной точке. Доказательство, примеры. Сжимающее отображение. Определение. Теорема Банаха о неподвижной точке. Доказательство, примеры. Метод Ньютона для решения нелинейных уравнений. Условия сходимости метода. Примеры. <br> |
| style="text-align:center;" | Тема 13. || Конечно-разностные уравнения и системы. || Формула Тейлора. Интерполяционный полином Лагранжа. Численная производная двухточечная и четырехточечная формулы для численной производной. Численное интегрирование. Оценки погрешностей численной производной и интеграла. Определение неподвижной точки. Теорема о неподвижной точке. Доказательство, примеры. Сжимающее отображение. Определение. Теорема Банаха о неподвижной точке. Доказательство, примеры. Метод Ньютона для решения нелинейных уравнений. Условия сходимости метода. Примеры. <br> |
||
| Line 75: | Line 75: | ||
'''Задания для практических занятий:</b>''' |
'''Задания для практических занятий:</b>''' |
||
{| |
{| |
||
| − | 1.Доказать, что в некоторой точке на интервале (-1;1) производная функции <math>f(x) = (1 - x^2)^{100}</math> равна 1. |
+ | :1.Доказать, что в некоторой точке на интервале (-1;1) производная функции <math>f(x) = (1 - x^2)^{100}</math> равна 1. |
</b> |
</b> |
||
| − | 2.Как повлияет на пропускную способность трубы со стационарным ламинарным течением жидкости а) удвоение перепада давления на концах трубы; б) удвоение диаметра трубы? |
+ | :2.Как повлияет на пропускную способность трубы со стационарным ламинарным течением жидкости а) удвоение перепада давления на концах трубы; б) удвоение диаметра трубы? |
</b> |
</b> |
||
| − | 3.Приведите определение метрического пространства, линейного нормированного пространства, евклидова пространства. Каковы соотношения между этими понятиями? |
+ | :3.Приведите определение метрического пространства, линейного нормированного пространства, евклидова пространства. Каковы соотношения между этими понятиями? |
</b> |
</b> |
||
| − | 4.Лестница прислоняется к трубе, как показано пунктиром на рисунке. Радиус трубы равен 1. Нижний конец лестницы находится в точке x=1+k/10. Определить координаты точки касания лестницы и трубы. Здесь k – номер студента в списке.</b> |
+ | :4.Лестница прислоняется к трубе, как показано пунктиром на рисунке. Радиус трубы равен 1. Нижний конец лестницы находится в точке x=1+k/10. Определить координаты точки касания лестницы и трубы. Здесь k – номер студента в списке.</b> |
[[File:t1.png|300px]]</b> |
[[File:t1.png|300px]]</b> |
||
| − | 5.Из плоскости вырезан круг радиуса 1 с центром в начале координат. Точка A=<1+Y/1000,0> на этой плоскости соединена натянутой нитью с точкой B=<0,1+Y/100>. Определить длину нити. При каком Y нить будет иметь форму отрезка?</b> |
+ | :5.Из плоскости вырезан круг радиуса 1 с центром в начале координат. Точка A=<1+Y/1000,0> на этой плоскости соединена натянутой нитью с точкой B=<0,1+Y/100>. Определить длину нити. При каком Y нить будет иметь форму отрезка?</b> |
| − | 6.Методом разделения переменных решить уравнение<math>\frac{{dx}}{{dt}} = Ax^\alpha</math> при <math>A = \pm Y</math>,α=0,1/2,1,2. Здесь Y – номер студента в списке. Под словом решить понимается описание общего решения при произвольных начальных данных. Для каждого из вариантов построить несколько траекторий. </b> |
+ | :6.Методом разделения переменных решить уравнение<math>\frac{{dx}}{{dt}} = Ax^\alpha</math> при <math>A = \pm Y</math>,α=0,1/2,1,2. Здесь Y – номер студента в списке. Под словом решить понимается описание общего решения при произвольных начальных данных. Для каждого из вариантов построить несколько траекторий. </b> |
| − | 7.Известно, что в момент <math>t_1 = 7</math> первая популяция имела численность 2Y, а вторая Y. Первая популяция возрастает со временем согласно уравнению <math>\frac{{dx}}{{dt}} = Yx</math>, а вторая <math>\frac{{dz}}{{dt}} = 2Yz</math>. В какой момент численности обеих популяций будут (или были) равными?</b> |
+ | :7.Известно, что в момент <math>t_1 = 7</math> первая популяция имела численность 2Y, а вторая Y. Первая популяция возрастает со временем согласно уравнению <math>\frac{{dx}}{{dt}} = Yx</math>, а вторая <math>\frac{{dz}}{{dt}} = 2Yz</math>. В какой момент численности обеих популяций будут (или были) равными?</b> |
| − | 8.Построить график решения уравнения <math>\frac{{dx}}{{dt}} = Yx^2</math> с начальным условием Y при <math>t_1 = 0</math>. В какие моменты решение будет в два раза больше и в два раза меньше начального значения?</b> |
+ | :8.Построить график решения уравнения <math>\frac{{dx}}{{dt}} = Yx^2</math> с начальным условием Y при <math>t_1 = 0</math>. В какие моменты решение будет в два раза больше и в два раза меньше начального значения?</b> |
| − | 9.Рассмотрим три дифференциальных уравнения первого порядка вида: <math>\frac{{dz}}{{dt}} = a|z|^b</math>, где a=2Y,_ b=1-Y/100,_ 1,_ 1+Y/100 с начальным условием при t=0: z(0)=Y. Методом разделения переменных найти решение в максимально возможных пределах в обе стороны по t. Существенен ли знак модуля в уравнении ? Построить графики решений.</b> |
+ | :9.Рассмотрим три дифференциальных уравнения первого порядка вида: <math>\frac{{dz}}{{dt}} = a|z|^b</math>, где a=2Y,_ b=1-Y/100,_ 1,_ 1+Y/100 с начальным условием при t=0: z(0)=Y. Методом разделения переменных найти решение в максимально возможных пределах в обе стороны по t. Существенен ли знак модуля в уравнении ? Построить графики решений.</b> |
| − | 10.Для уравнения фон Берталанфи с α=1,_ β=Y определить время удвоения объема при различных начальных данных.</b> |
+ | :10.Для уравнения фон Берталанфи с α=1,_ β=Y определить время удвоения объема при различных начальных данных.</b> |
| − | 11.Для уравнения Гомперца финальная масса вдвое больше начальной. Временной масштаб λ=Y. Определить константу r.</b> |
+ | :11.Для уравнения Гомперца финальная масса вдвое больше начальной. Временной масштаб λ=Y. Определить константу r.</b> |
| − | 12.Привести к диагональному виду оператор с матрицей A=</b> [[File:t2.png|300px]]</b> |
+ | :12.Привести к диагональному виду оператор с матрицей A=</b> [[File:t2.png|300px]]</b> |
| − | 13.Решить систему дифференциальных уравнений <math>\frac{{d\vec{X}}}{{dt}} = A\vec{X}</math> с упомянутой выше матрицей А и начальным условием X ⃗(0)=<0,0,0,1>. Построить графики компонент решения на отрезке [0,3].</b> |
+ | :13.Решить систему дифференциальных уравнений <math>\frac{{d\vec{X}}}{{dt}} = A\vec{X}</math> с упомянутой выше матрицей А и начальным условием X ⃗(0)=<0,0,0,1>. Построить графики компонент решения на отрезке [0,3].</b> |
| − | 14.То же задание для системы с матрицей B=A-2E, E – единичная матрица.</b> |
+ | :14.То же задание для системы с матрицей B=A-2E, E – единичная матрица.</b> |
| − | 15.Ответить еще раз на вопросы 8-10, используя метод Рунге - Кутты. Сравнить полученные графики с аналитическими. Исследовать зависимость погрешности численного решения от шага схемы Р-К и времени интегрирования.</b> |
+ | :15.Ответить еще раз на вопросы 8-10, используя метод Рунге - Кутты. Сравнить полученные графики с аналитическими. Исследовать зависимость погрешности численного решения от шага схемы Р-К и времени интегрирования.</b> |
| − | 16.В шар объемом V вписан цилиндр. При каком радиусе объем цилиндра максимален? При каком радиусе максимальна площадь его поверхности ?</b> |
+ | :16.В шар объемом V вписан цилиндр. При каком радиусе объем цилиндра максимален? При каком радиусе максимальна площадь его поверхности ?</b> |
| − | 17.Чтобы удержать груз на канате, перекинутом через балку, нужна сила ≥10кг, а чтобы начать подтягивать на свою сторону ≥10+ Y кг. Определить вес груза. Определить коэффициент трения, если угол обхвата <math>\omega = 10Y</math> градусов.</b> |
+ | :17.Чтобы удержать груз на канате, перекинутом через балку, нужна сила ≥10кг, а чтобы начать подтягивать на свою сторону ≥10+ Y кг. Определить вес груза. Определить коэффициент трения, если угол обхвата <math>\omega = 10Y</math> градусов.</b> |
| − | 18.В следующих задачах начальные данные <x,y> для системы двух дифференциальных уравнений первого порядка [[File:t4.png|200px]] пробегают единичную окружность: <math>x^2(0) + y^2(0) = 1</math>. Требуется описать (и нарисовать кривые – геометрическое место точек) множество решений в следующие моменты времени t=-1, 1, 2. Для ориентировки: если А – нулевая матрица, то все три искомые кривые совпадают с единичной окружностью, а если А – единичная матрица, то это окружности радиуса e^t. Для каждой задачи указать, имеется ли у системы первый интеграл?</b> |
+ | :18.В следующих задачах начальные данные <x,y> для системы двух дифференциальных уравнений первого порядка [[File:t4.png|200px]] пробегают единичную окружность: <math>x^2(0) + y^2(0) = 1</math>. Требуется описать (и нарисовать кривые – геометрическое место точек) множество решений в следующие моменты времени t=-1, 1, 2. Для ориентировки: если А – нулевая матрица, то все три искомые кривые совпадают с единичной окружностью, а если А – единичная матрица, то это окружности радиуса e^t. Для каждой задачи указать, имеется ли у системы первый интеграл?</b> |
[[File:t3.png|500px]]</b> |
[[File:t3.png|500px]]</b> |
||
| − | 19.Для уравнений химической кинетики при <math>\nu = \mu = 1, \quad k1 = 1, \quad k2 = 2</math> на фазовой области описать множество начальных условий, для которых реакция полностью заканчивается за время Y.</b> |
+ | :19.Для уравнений химической кинетики при <math>\nu = \mu = 1, \quad k1 = 1, \quad k2 = 2</math> на фазовой области описать множество начальных условий, для которых реакция полностью заканчивается за время Y.</b> |
| − | 20.Пружинный маятник с трением описывается уравнением <math>\ddot{x} + k\dot{x} + \omega^2x = 0</math>. Пусть <math>\omega = 1, \quad k = 2 \pm \frac{Y}{100}</math>. Построить графики решения при нескольких различных начальных данных. Построить фазовые портреты.</b> |
+ | :20.Пружинный маятник с трением описывается уравнением <math>\ddot{x} + k\dot{x} + \omega^2x = 0</math>. Пусть <math>\omega = 1, \quad k = 2 \pm \frac{Y}{100}</math>. Построить графики решения при нескольких различных начальных данных. Построить фазовые портреты.</b> |
| − | 21.Длина физического маятника без трения Y см. Ускорение свободного падения g=9,8 м/сек^2. Определить период малых колебаний. Численно определить амплитуду колебаний при которых период вдвое и втрое больше. Для уравнения идеального маятника <math>\frac{{d^2x}}{{dt^2}} + Y \sin{x} = 0</math> энергетическим методом построить траектории. Интеграл для периода колебаний вычислить методом Симпсона. Построить график зависимости периода колебаний от его амплитуды.</b> |
+ | :21.Длина физического маятника без трения Y см. Ускорение свободного падения g=9,8 м/сек^2. Определить период малых колебаний. Численно определить амплитуду колебаний при которых период вдвое и втрое больше. Для уравнения идеального маятника <math>\frac{{d^2x}}{{dt^2}} + Y \sin{x} = 0</math> энергетическим методом построить траектории. Интеграл для периода колебаний вычислить методом Симпсона. Построить график зависимости периода колебаний от его амплитуды.</b> |
| − | 22.Построить методом Рунге – Кутты траектории (несколько - с разными начальными данными) для уравнения маятника с трением <math>\frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Y\sin{x} = 0</math>.</b> |
+ | :22.Построить методом Рунге – Кутты траектории (несколько - с разными начальными данными) для уравнения маятника с трением <math>\frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Y\sin{x} = 0</math>.</b> |
| − | 23.Тот же вопрос для <math>\frac{{d^2x}}{{dt^2}} + 11\frac{{dx}}{{dt}} + Y\sin{x} = 0</math></b> |
+ | :23.Тот же вопрос для <math>\frac{{d^2x}}{{dt^2}} + 11\frac{{dx}}{{dt}} + Y\sin{x} = 0</math></b> |
| − | 24.Для уравнения <math>\frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx = \sin{\omega t}</math> подобрать частоту <math>\omega</math> так, чтобы амплитуда вынужденных колебаний была максимальна. Построить графики и траектории для решения (с нулевыми начальными условиями) для этой частоты, а также для <math>\frac{{\omega}}{2}</math> и <math>2\omega</math>. |
+ | :24.Для уравнения <math>\frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx = \sin{\omega t}</math> подобрать частоту <math>\omega</math> так, чтобы амплитуда вынужденных колебаний была максимальна. Построить графики и траектории для решения (с нулевыми начальными условиями) для этой частоты, а также для <math>\frac{{\omega}}{2}</math> и <math>2\omega</math>. |
| − | 25.Построить траектории для уравнения <math>\frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx^3 = \sin{\omega t}</math></b> |
+ | :25.Построить траектории для уравнения <math>\frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx^3 = \sin{\omega t}</math></b> |
| − | 26.Пусть функция <math>\Psi</math> - ступенчатая, попеременно на отрезках равной длины принимающая значения 1 и -1, <math>\Psi(s) = \text{sign}\sin(s)</math>. |
+ | :26.Пусть функция <math>\Psi</math> - ступенчатая, попеременно на отрезках равной длины принимающая значения 1 и -1, <math>\Psi(s) = \text{sign}\sin(s)</math>. |
| − | 27.Для уравнения <math>\frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx = \Psi(\omega t)</math>подобрать частоту <math>\omega</math> так, чтобы амплитуда вынужденных колебаний была максимальна. Построить графики и траектории для решения (с нулевыми начальными условиями) для этой частоты, а также для <math>\frac{\omega}{2}</math> и <math>2\omega</math>.</b> |
+ | :27.Для уравнения <math>\frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx = \Psi(\omega t)</math>подобрать частоту <math>\omega</math> так, чтобы амплитуда вынужденных колебаний была максимальна. Построить графики и траектории для решения (с нулевыми начальными условиями) для этой частоты, а также для <math>\frac{\omega}{2}</math> и <math>2\omega</math>.</b> |
| − | 28.Построить траектории для уравнения <math>\frac{d^2x}{dt^2} + \frac{dx}{dt} + Yx^3 = \Psi(\omega t)</math>.</b> |
+ | :28.Построить траектории для уравнения <math>\frac{d^2x}{dt^2} + \frac{dx}{dt} + Yx^3 = \Psi(\omega t)</math>.</b> |
| − | 29.Определить численно зависимость периода и сдвига фаз между компонентами решения от амплитуды периодических решений системы Лотки – Вольтера при <math>\alpha = \beta = \gamma = 1, \quad \delta = Y</math>. Построить графики решений для нескольких вариантов начальных данных.</b> |
+ | :29.Определить численно зависимость периода и сдвига фаз между компонентами решения от амплитуды периодических решений системы Лотки – Вольтера при <math>\alpha = \beta = \gamma = 1, \quad \delta = Y</math>. Построить графики решений для нескольких вариантов начальных данных.</b> |
| − | 30.Для уравнений химической кинетики построить графики зависимости решения от времени при <math>\nu = 1, \quad \mu = 2, \quad k1 = 10, \quad k2 = Y, \quad n1(0) = 5, \quad n2(0) = 7</math>.</b> |
+ | :30.Для уравнений химической кинетики построить графики зависимости решения от времени при <math>\nu = 1, \quad \mu = 2, \quad k1 = 10, \quad k2 = Y, \quad n1(0) = 5, \quad n2(0) = 7</math>.</b> |
| + | :31.Для многочлена <math>P(x) = x^3 + \alpha x^2 + Yx</math> определить значения <math>\alpha_*</math>, при которых имеется вырожденная стационарная точка. Как различаются многочлены со значениями <math>\alpha</math> по разные стороны от <math>\alpha_*</math>? Построить графики для примеров. |
||
| ⚫ | |||
| + | :32.Параметрическим называется резонанс вследствие изменения коэффициентов уравнения. Для уравнения второго порядка <math>x'' + x' + Y(1 + a\sin{\omega t})x = 0</math> численным экспериментом определить, при каких значениях параметров <math>a, \omega</math> теряется устойчивость состояния покоя ? Указать границы областей параметров, где ПР наблюдается. Для нескольких вариантов параметров построить графики решения. |
||
| ⚫ | |||
| + | :33.Пусть каждая пара бессмертных кроликов на первом месяце не рожает, на втором месяце рожает (Y+1) пару, а потом каждый месяц по одной. Найти характеристические числа соответствующего уравнения (график характеристического многочлена построить). Оценить численность популяции спустя много месяцев и сравнить с результатом, полученным прямым вычислением (построить график разности). Вначале была 1 пара, только что родившаяся. |
||
| ⚫ | |||
| + | :34.Для системы уравнений Лотки - Вольтерры с параметрами из задачи 31 определить погрешность (изменение первого интеграла в конечный момент времени по отношению к начальному) в зависимости от периода и шага разностной схемы Рунге - Кутты 4-го порядка с постоянным шагом. Время интегрирования – 100 периодов. |
||
| ⚫ | |||
| + | :35.Использовать экстраполяционный метод Ричардсона для уменьшения этой погрешности. В каком диапазоне шагов метод неэффективен и почему? |
||
| ⚫ | |||
| + | :36.Привести пример линейной системы дифференциальных уравнений с постоянными коэффициентами, для которой начало координат асимптотически устойчиво и существуют решения, модуль которых сначала растет, а потом убывает. Привести графики компонент и модуля таких решений. Возможно ли, чтобы все решения системы с асимптотически устойчивой стационарной точкой обладали таким свойством немонотонности? |
||
| ⚫ | |||
| + | :37.Пусть <math>f(x, y) = \sin{x} + \cos{(x + Yy)}</math>. С помощью леммы Морса исследовать поведение функции в окрестности стационарных (критических) точек. Нарисовать изолинии f. |
||
| ⚫ | |||
| + | :38.Пусть<math>f(x, y, z) = \sin{x} + \cos{(x + Yy)} + \sin{(x + Yy + Y^2z)}</math> Исследовать поведение функции в окрестности стационарных точек. |
||
| ⚫ | |||
| + | :39.Исследовать системы <math>\dot{x} = y \pm Yy^2, \quad \dot{y} = -x \pm x^2</math> методом разделения переменных. Устойчивы ли стационарные точки этих систем? Сопоставить с исследованием устойчивости методом Ляпунова. |
||
| − | |} |
||
| + | :40.Для уравнения пружинного маятника с трением <math>\ddot{x} + \text{sign}(\dot{x}) + Yx = 0</math> с начальным условием <Y,Y> определить число колебаний до остановки. |
||
| + | :41. Методом Ньютона исследовать уравнение <math>\sin{z} = Yz, \quad z \in \mathbb{C}</math> |
||
| + | :42.Рассмотрим линейный дифференциальный оператор <math>(x^2 + 3x - Y)\frac{d^2}{dx^2} + (2x - 7)\frac{d}{dx}</math>. Докажите, что он оставляет инвариантным подпространство многочленов степени не выше 10. Вычислить матрицу этого оператора в базисе, составленном из этих 11 мономов. Вычислить спектр этого оператора. То же для многочленов степени не выше 12. |
||
| + | :43.Для дифф. уравнения Бесселя степени 2: <math>r^{-1}\frac{d}{dr}r\frac{d}{dr}u + (Y-4r^{-2})u = 0</math> построить решение, ограниченное в нуле. При малых r строить разложением в ряд Ньютона, а потом при некотором <math>r = \varepsilon</math> использовать полученные <math>u(\varepsilon), \quad u'(\varepsilon)</math>в качестве начальных данных для метода Рунге - Кутты, каковым интегрировать до 10/\sqrt Y. Оценить зависимость погрешности от числа членов ряда Ньютона, выбора <math>\varepsilon</math> и шага схемы. Применить метод Ричардсона для повышения точности. |
||
| + | :44.Для сетки {-Y,0,1,2,3} построить многочлен степени 5, который во всех узлах обращается в нуль, а первая производная которого в левой точке равна 1. То же для правой точки. Построить графики. |
||
| + | :45.На единичной окружности <math>x \in [0, 2\pi)</math>задана равномерная сетка из Y+10 точек. Значения сеточной функции равны значениям функции sin(x). Вычислить в точках сетки первую и вторую производные по компактной схеме и сравнить с истинным результатом. Построить графики. |
||
| + | :46.На маятник сбоку дует ветер. Поэтому уравнение для его колебаний принимает вид: <math>\ddot{x} + A\sin{x} + B\cos{x} = 0</math>. Нужно a) Объяснить физический смысл В; b) Построить фазовый портрет и проинтегрировать уравнение при А=1, В=Y. c)При этих же значениях параметров определить зависимость периода от амплитуды и сравнить со случаем В=0. |
||
| + | :47.Для уравнения маятника с трением <math>\frac{d^2x}{dt^2} + \frac{dx}{dt} + Yx = 0</math> рассмотрим решения с начальными данными <1,0> и <0,1>. На фазовой плоскости построить соответствующие параллелограммы при t=-1, 1, 3. Построить график зависимости вронскиана от времени. |
||
| + | :48. То же для начальных данных в круге <math>(x - Y)^2 + \dot{x}^2 < \frac{Y}{2}</math>. Приложить распечатку программы. |
||
| + | :49.Для уравнения <math>\frac{d^2x}{dt^2} + \frac{dx}{dt} + Y(x + \varepsilon \sin{x}) = 0</math>, зависящего от параметра<math>\varepsilon</math> рассмотрим решения с начальными данными <1,0> и <0,1>. На фазовой плоскости построить для |t|< 1 решения при <math>\varepsilon=0, 0.01, 0.02</math>. Построить разности решений для 0,01 и 0, для 0,02 и 0. Построить решения для уравнения в вариациях, полагая <math>\varepsilon \rightarrow 0</math>. Для тех же значений <math>\varepsilon==0,_0,01,_0,02</math>. вычислить его решение. Сравнить оба метода. Оценить скорость нарастания погрешности метода уравнения в вариациях со временем. |
||
| + | :50. Для уравнения второго порядка <math>x'' + x' + Y(1 + a\sin{\omega t})x = 0</math> численным экспериментом определить, в зависимости от значений параметров <math>a, \quad \omega</math> след и определитель матрицы монодромии. Определите мультипликатор с наибольшим модулем. Постройте кривые, на которых он равен 1, - они являются границами устойчивости нулевого решения (и параметрического резонанса). Сопоставить с результатами задачи, полученными в 53. |
||
| + | :51.Для уравнения <math>\ddot{x} + Yx = f(t)</math> методом вариации постоянных получить общее решение. |
||
| + | :52.Шарик с нулевой начальной скоростью под действием силы тяжести без трения движется под действием силы тяжести по желобу, имеющему форму параболы, причем z(0)=1, z(Y)=0. Требуется с помощью численных экспериментов определить, какая из парабол обеспечивает наименьшее время для достижения конечной точки. |
||
| + | :53. Рассмотрим гамильтонову систему с двумя степенями свободы с гамильтонианом |
||
| + | <math>H(x_1, x_2, p_1, p_2) = \frac{1}{2}c(\vec{x})|p|^2 - \frac{1}{2}c^{-1}(\vec{x})</math> Выписать систему Гамильтона. Траектории этой гамильтоновой системы (бихарактеристики), точнее их проекции на плоскость <x_1,x_2>, описывают движение лучей в среде с переменной скоростью с. Докажите, что при с=const лучи – прямые. Если рассматривается точечный источник лучей (скажем, из начала координат), то начальные данные образуют двумерное подпространство <0,0,p_1,p_2>. Предположим, что среда «слоистая»: <math> |
||
| + | c = f(x2) = \begin{cases} 1 & \text{if } |x2| > 1 \\ 1 + Y\sin{\pi x_2} & \text{if } |x_2| < 1 \end{cases} |
||
| + | </math>. Вычислить геометрию лучей. Определить критический угол <math>\alpha = \left|\arctan{\frac{p_1(0)}{p_2(0)}}\right|</math>, при котором лучи не покидают волновод <math>|x_2| < 1</math>. |
||
| + | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
=== Перечень учебно-методического обеспечения дисциплины === |
=== Перечень учебно-методического обеспечения дисциплины === |
||
| Line 254: | Line 280: | ||
| style="vertical-align:middle; text-align:center;" | Устный/письменный опрос |
| style="vertical-align:middle; text-align:center;" | Устный/письменный опрос |
||
| style="vertical-align:middle; text-align:left;" | Отвечать, максимально полно, логично и структурировано, на поставленный вопрос. Основная цель – показать всю глубину знаний по конкретной теме или ее части. |
| style="vertical-align:middle; text-align:left;" | Отвечать, максимально полно, логично и структурировано, на поставленный вопрос. Основная цель – показать всю глубину знаний по конкретной теме или ее части. |
||
| − | |- |
||
| − | | style="vertical-align:middle; text-align:center;" | Реферат |
||
| − | | style="vertical-align:middle; text-align:left;" | Поиск источников и литературы, составление библиографии. При написании реферата рекомендуется использовать разнообразные источники, монографии и статьи из научных журналов, позволяющие глубже разобраться в различных точках зрения на заданную тему. Изучение литературы следует начинать с наиболее общих трудов, затем следует переходить к освоению специализированных исследований по выбранной теме. Могут быть использованы ресурсы сети «Интернет» с соответствующими ссылками на использованные сайты.<br>Если тема содержит проблемный вопрос, следует сформулировать разные точки зрения на него. Рекомендуется в выводах указать свое собственное аргументированное мнение по данной проблеме. Подготовить презентацию для защиты реферата. |
||
| − | |- |
||
| − | | style="vertical-align:middle; text-align:center;" | Эссе |
||
| − | | style="vertical-align:middle; text-align:left;" | Написание прозаического сочинения небольшого объема и свободной композиции, выражающего индивидуальные впечатления и соображения по конкретному поводу или вопросу и заведомо не претендующего на определяющую или исчерпывающую трактовку предмета. При работе над эссе следует четко и грамотно формулировать мысли, структурировать информацию, использовать основные понятия, выделять причинно-следственные связи. Как правило эссе имеет следующую структуру: вступление, тезис и аргументация его, заключение. В качестве аргументов могут выступать исторические факты, явления общественной жизни, события, жизненные ситуации и жизненный опыт, научные доказательства, ссылки на мнение ученых и др. |
||
|- |
|- |
||
| style="vertical-align:middle; text-align:center;" | Подготовка к промежуточной аттестации |
| style="vertical-align:middle; text-align:center;" | Подготовка к промежуточной аттестации |
||
| style="vertical-align:middle; text-align:left;" | При подготовке к промежуточной аттестации необходимо проработать вопросы по темам, которые рекомендуются для самостоятельной подготовки. При возникновении затруднений с ответами следует ориентироваться на конспекты лекций, семинаров, рекомендуемую литературу, материалы электронных и информационных справочных ресурсов, статей.<br>Если тема вызывает затруднение, четко сформулировать проблемный вопрос и задать его преподавателю. |
| style="vertical-align:middle; text-align:left;" | При подготовке к промежуточной аттестации необходимо проработать вопросы по темам, которые рекомендуются для самостоятельной подготовки. При возникновении затруднений с ответами следует ориентироваться на конспекты лекций, семинаров, рекомендуемую литературу, материалы электронных и информационных справочных ресурсов, статей.<br>Если тема вызывает затруднение, четко сформулировать проблемный вопрос и задать его преподавателю. |
||
| − | |- |
||
| − | | style="vertical-align:middle; text-align:center;" | Практические (лабораторные) занятия |
||
| − | | style="vertical-align:middle; text-align:left;" | Практические занятия предназначены прежде всего для разбора отдельных сложных положений, тренировки аналитических навыков, а также для развития коммуникационных навыков. Поэтому на практических занятиях необходимо участвовать в тех формах обсуждения материала, которые предлагает преподаватель: отвечать на вопросы преподавателя, дополнять ответы других студентов, приводить примеры, задавать вопросы другим выступающим, обсуждать вопросы и выполнять задания в группах. Работа на практических занятиях подразумевает домашнюю подготовку и активную умственную работу на самом занятии. Работа на практических занятиях в форме устного опроса заключается прежде всего в тренировке навыков применять теоретические положения к самому разнообразному материалу. В ходе практических занятий студенты работают в группах для обсуждения предлагаемых вопросов. |
||
|- |
|- |
||
| style="vertical-align:middle; text-align:center;" | Самостоятельная работа |
| style="vertical-align:middle; text-align:center;" | Самостоятельная работа |
||
| style="vertical-align:middle; text-align:left;" | Самостоятельная работа состоит из следующих частей: 1) чтение учебной, справочной, научной литературы; 2) повторение материала лекций; 3) составление планов устных выступлений; 4) подготовка видеопрезентации. При чтении учебной литературы нужно разграничивать для себя материал на отдельные проблемы, концепции, идеи. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис. |
| style="vertical-align:middle; text-align:left;" | Самостоятельная работа состоит из следующих частей: 1) чтение учебной, справочной, научной литературы; 2) повторение материала лекций; 3) составление планов устных выступлений; 4) подготовка видеопрезентации. При чтении учебной литературы нужно разграничивать для себя материал на отдельные проблемы, концепции, идеи. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис. |
||
| − | |- |
||
| − | | style="vertical-align:middle; text-align:center;" | Видеопрезентация |
||
| − | | style="vertical-align:middle; text-align:left;" | Подготовка видеопрезентаций по курсу. Видеопрезентации могут быть сделаны на любую тему, затронутую в ходе курса. Темы должны быть заранее согласованы с преподавателем. Видеопрезентации продолжительностью около 5 минут (300 секунд) должны быть подготовлены в группах, определяемых преподавателем. Несмотря на то, что это групповая работа, должен явно присутствовать вклад каждого члена группы. |
||
| − | |- |
||
| − | | style="vertical-align:middle; text-align:center;" | Доклад |
||
| − | | style="vertical-align:middle; text-align:left;" | Публичное, развернутое сообщение по определенной теме или вопросу, основанное на документальных данных. При подготовке доклада рекомендуется использовать разнообразные источники, позволяющие глубже разобраться в теме. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис. |
||
| − | |- |
||
| − | | style="vertical-align:middle; text-align:center;" | Дискуссия |
||
| − | | style="vertical-align:middle; text-align:left;" | Публичное обсуждение спорного вопроса, проблемы. Каждая сторона должна оппонировать мнение собеседника, аргументируя свою позицию. |
||
|- |
|- |
||
| style="vertical-align:middle; text-align:center;" | Контрольная работа |
| style="vertical-align:middle; text-align:center;" | Контрольная работа |
||
| style="vertical-align:middle; text-align:left;" | При подготовке к контрольной работе необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. |
| style="vertical-align:middle; text-align:left;" | При подготовке к контрольной работе необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. |
||
| − | |- |
||
| − | | style="vertical-align:middle; text-align:center;" | Тестирование (устное/письменное) |
||
| − | | style="vertical-align:middle; text-align:left;" | При подготовке к тестированию необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. Основная цель тестирования – показать уровень сформированности знаний по конкретной теме или ее части. |
||
| − | |- |
||
| − | | style="vertical-align:middle; text-align:center;" | Индивидуальная работа |
||
| − | | style="vertical-align:middle; text-align:left;" | При выполнение индивидуальной работы необходимо взять задание у преподавателя, ознакомиться с требованиями к выполнению работы, изучить поставленную проблему, найти решение проблемы. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия. Оформить результаты работы. |
||
|- |
|- |
||
| style="vertical-align:middle; text-align:center;" | Разработка отдельных частей кода |
| style="vertical-align:middle; text-align:center;" | Разработка отдельных частей кода |
||
Latest revision as of 16:18, 6 April 2024
Обыкновенные дифференциальные уравнения
- Квалификация выпускника: бакалавр
- Направление подготовки: 09.03.01 - “Информатика и вычислительная техника”
- Направленность (профиль) образовательной программы: Математические основы ИИ
- Программу разработал(а): В.А.Гордин
1. Краткая характеристика дисциплины
Курс «Дифференциальные уравнения» включает в себя основные теоремы, аналитические методы исследования уравнений и систем, дифференциальных и разностных, основные методы численного решения начальных и краевых задач, примеры практических задач, сводящихся к качественному исследованию или численному решению дифференциальных уравнений или систем.
Данный курс должен помочь студентам воспринимать динамические модели и задачи оптимизации, изучаемые по данной специальности, а в будущем – самостоятельно разрабатывать, анализировать и обсчитывать аналогичные модели и задачи такого рода.
Студентам в дальнейшем предстоит, в частности, изучать задачи оптимизации (вариационное исчисление и принцип максимума Понтрягина), сводящиеся к решению обыкновенных уравнений или систем. Некоторые из методов, изучаемых в курсе, будут изучаться студентами более подробно в курсах оптимизации, численных методов и уравнений в частных производных. Данный курс должен дать для этого надлежащую подготовку.
Ко многим разделам курса будут предлагаться геометрические иллюстрации и примеры экономического, экологического, социологического и физического содержания.
2. Перечень планируемых результатов обучения
- Целью освоения дисциплины является знакомство студентов с основными идеями и конструкциями теории обыкновенных дифференциальных и разностных уравнений и систем, их геометрическими интерпретациями и приложениями к прикладным задачам, методами их составления, анализа и численного определения решений.
- Задачами дисциплины являются изучение методов теории дифференциальных и разностных уравнений для построения математических моделей различных явлений и их качественного и количественного анализа.
- Пререквизиты (Предварительные знания у слушателей)
Изучение курса «Дифференциальные уравнения» требует предварительные знания по математическому анализу, линейной алгебре и аналитической геометрии в объеме, предусмотренном программой обучения за 1 курс, а также навыков программирования. Он читается параллельно с продолжающимися курсами математического анализа и программирования – знания и навыки, получаемый там, будут использоваться в данном курсе. Содержание программы по математике за среднюю школу предполагается безусловно известным.
Предполагается владение математическим анализом в полном объеме, линейной алгеброй в объеме книги И.М.Гельфанда «Лекции по линейной алгебре» кроме главы о тензорах, теория обыкновенных дифференциальных уравнений, владение вычислительной математикой в объеме обязательного курса, элементарные сведения из теории вероятностей, умение программировать в среде МАТЛАБ или на Пайтоне. Желательно владение функциональным анализом в объеме элективного курса.
Общая характеристика результата обучения по дисциплине
- Знания: сформированы систематические знания об основных типах ОДУ и моделях, на них основанных, систематические навыки качественного исследования ОДУ и некоторые сведения и навыки по численному их решению.
- Умения: сформированы умения оценивать корректность задач, использующих ОДУ, проводить качественный анализ решения, а в некоторых случаях находить аналитически явные решения, строить алгоритмы численного решения, проводить анализ точности полученных решений и их грубости по отношению к шумам в исходных данных.
3. Структура и содержание дисциплины
| № п/п |
Наименование раздела дисциплины |
Содержание дисциплины по темам |
| Тема 1. | Введение. Простейшие дифференциальные и разностные уравнения. | Интегрирование – метод решения уравнения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u'=f(x)}
. Стационарное течение жидкости в трубе. Ламинарный и турбулентный режимы. Формула Пуазейля. Число Рейнольдса – безразмерный параметр задачи. Проблемы граничных условий. Течение в кровеносных сосудах. Простейшие дифференциальные и разностные уравнения: модель Мальтуса, движение материальной точки по потоку ветра или течения, дискретное и непрерывное нарастание процента, радиоактивный распад. Решение простейших уравнений. Классификация обыкновенных дифференциальных уравнений и систем: разрешимость (неразрешимость) относительно старшей производной, автономность (автономность), линейность (нелинейность) уравнений и систем. Устойчивость или неустойчивость нулевого решения. Векторное поле – правая часть системы дифференциальных уравнений первого порядка. Примеры. Итерационные процессы (рекуррентные формулы): банковский процент, последовательность Фибоначчи, метод Герона. Метод Ньютона, его модификации и обобщения. Бассейны притяжения в случаях квадратного и кубического уравнений. |
| Тема 2. | Задача Коши. Существование, единственность, корректность. | Сведение дифференциального уравнения к интегральному уравнению Вольтерры. Сжимающее отображение в пространстве функций. Примеры решения дифференциального уравнения итерационным методом Пикара – Линделефа. Теорема Пеано существования решения задачи Коши «в малом» (без док.). Примеры неединственности решения задачи Коши. Теорема существования и единственности, если правая часть липшиц-непрерывна «в малом»; корректность задачи Коши (без док.). Уравнения в вариациях. Пример несуществования решения «в большом». Решение задачи Коши для дифференциального уравнения, разрешенного относительно старшей производной, с помощью рядов Тейлора. Примеры. Ряд Тейлора для решения уравнения Бесселя. |
| Тема 3. | Метод разделения переменных. | Теорема об обратной функции. Метод разделения переменных для решения уравнения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dx} = f(y)}
и для уравнения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dx} = f(y) \cdot g(x)}
. Примеры. Истечение воды из воронки переменного сечения. Вывод уравнения и его решение. Ограничения модели. Уравнение фон Берталанфи. Точное решение и качественное исследование. Оценка параметров модели по экспериментальным данным. Уравнение Гомпертца. Точное решение и качественное исследование. Оценка параметров модели по экспериментальным данным. Логистическое уравнение Ферхюльста. Разностный вариант. Бифуркации в периодический и хаотический режимы. Жесткий и мягкий планы лова рыбы. . |
| Тема 4. | Линейные уравнения и системы с постоянными и переменными коэффициентами. | Приведение линейной системы с постоянными коэффициентами к каноническому виду. Общее решение системы линейных уравнений с постоянными коэффициентами, однородных и неоднородных – подпространство и плоскость. Принцип суперпозиции. Сведение уравнения с постоянными коэффициентами к системе. Всегда ли возможно обратное? Характеристический многочлен. Неоднородные дифференциальные уравнения. Экспонента, синус и гиперсинус в правой части. Возможность резонанса. Жорданова клетка в правой части системы дифференциальных уравнений с постоянными коэффициентами. Функции от матрицы. Решение в виде экспоненты оператора. Введение в операционное исчисление (преобразование Лапласа). Показание измерительного прибора с учетом его инерции. Динамика показаний инерционного прибора при синусоидальном воздействии. Модели войны армий и орд. Условие в модели войны орд неединственности стационарной точки. Существование и отсутствие первого интеграла. Сепаратриса. Уравнение трения каната о бревно. Вывод и точное решение ОДУ. Формула Эйлера. Классификация линейных двумерных систем ОДУ. Фундаментальная система решений (ФСР) для произвольных линейных уравнения или системы. Теория Вронского. Метод Лагранжа вариации постоянных для неоднородных уравнений и систем. |
| Тема 5. | Первые интегралы и фазовые портреты. | Уравнения химической кинетики. Первый интеграл. Варианты завершения процесса. Интегрирование системы. Пружинный маятник. Физический маятник без трения. Фазовые портреты. Первый интеграл. Устойчивые и неустойчивые стационарные точки. Колебательный и вращательный режимы. Автономные нелинейные уравнения второго порядка «без трения». Первый интеграл и фазовый портрет. Возможные типы стационарных (критических) точек первого интеграла. Лемма Морса (без док.). Маятник с трением. Убывание интеграла механической энергии. Фазовый портрет. Неустойчивость и асимптотическая устойчивость стационарной точки. Маятник с трением и форсингом. Фазовый портрет. Предельный цикл. Примеры систем с устойчивыми и неустойчивыми предельными циклами. Сечение Пуанкаре для проверки устойчивости предельных циклов. Мультипликаторы. Зависимость амплитуды периодического решения от частоты гармонического форсинга. Связь коэффициента трения и ширины резонансной кривой. Дифференциальное уравнение с разрывной правой частью. Пружинный маятник с трением о стол. Определение аттрактора этой системы. Понятие системы в общем положении; примеры. Аттрактор системы в общем положении для динамических систем размерности 2 и 3. |
| Тема 6. | Простейшие экологические модели. | Логистическое уравнение. Устойчивая и неустойчивая стационарная точки. Возможные границы отлова. Жесткая и мягкая модели. Опасность оптимизации в жесткой модели. Гибкие планы отлова. Модель Лотки – Вольтера. Стационарные точки и исследование их устойчивости. Первый интеграл системы (два способа построения). Сравнение теории с экспериментальными данными. Ограничения модели. Задача о двух видах, конкурирующих за общий ресурс. |
| Тема 7. | Конечно-разностные уравнения и системы. | Последовательность Фибоначчи. Конечно-разностные уравнения и системы. Пространство решений линейного конечно-разностного уравнения n-го порядка n-мерно. Общее решение для уравнения с постоянными коэффициентами. Случаи простых и кратных корней характеристического уравнения. Матрица Лесли и предельное распределение популяции по возрастам. Игра с конечной суммой (блуждание частицы). Марковские цепи. Пример нелинейного конечно-разностного уравнения. Метод Герона и метод Ньютона. Метод Ньютона и сверхсжатие для некратных корней. |
| Тема 8. | Устойчивость и неустойчивость стационарных точек систем. | Устойчивость положения равновесия при t→+∞ для дифференциальных и разностных систем с постоянными коэффициентами. Теория Ляпунова – исследование устойчивости стационарных точек нелинейных систем (без док.). Примеры, когда спектральный метод бессилен. Метод функции Ляпунова. |
| Тема 9. | Введение в разностные схемы для решения задачи Коши. | Разностные схемы для решения задачи Коши. Схема Эйлера, Эйлера с пересчетом, схема центральных разностей. Схемы Рунге – Кутты. Метод экстраполяции Ричардсона для повышения точности схемы. |
| Тема 10. | Семейства траекторий и решение типа бегущей волны. | Уравнение в вариациях. Гомотопия. Метод стрельбы (пристрелки) для решения краевой задачи. Изменение фазового объема в окрестности траектории. Дивергенция векторного поля. Теорема Лиувилля, спектр матрицы системы и разбегание траекторий. Вывод уравнения неразрывности. Характеристики. Уравнение переноса и решение типа бегущей волны. Неоднородное уравнение переноса и изменение решения вдоль характеристики. Применение фундаментальной системы решений к интегрированию неоднородных систем – метод Лагранжа вариации постоянных. |
| Тема 11. | Специальные типы систем ОДУ. | Теория Флоке. Матрица монодромии и мультипликаторы. Анализ устойчивости для решений уравнений с периодическими коэффициентами. Гамильтоновы системы. Сохранение гамильтониана. Сохранение фазового объема. Примеры. Принцип наименьшего действия. |
| Тема 12. | Сингулярные возмущения и релаксационные колебания. | Системы вида Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon d_t\overrightarrow{X}^\varepsilon = \vec{g}(\vec{X}^\varepsilon, \vec{Y}^\varepsilon, \varepsilon)}
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_t\overrightarrow{Y}^\varepsilon = \vec{f}(\vec{X}^\varepsilon, \vec{Y}^\varepsilon, \varepsilon)}
, где Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < \varepsilon \ll 1}
.Поверхность вырождения: устойчивые и неустойчивые участки. Фазовый портрет. Чередование быстрых и медленных движений. Периодические режимы. Уравнение Ван дер Поля. |
| Тема 13. | Конечно-разностные уравнения и системы. | Формула Тейлора. Интерполяционный полином Лагранжа. Численная производная двухточечная и четырехточечная формулы для численной производной. Численное интегрирование. Оценки погрешностей численной производной и интеграла. Определение неподвижной точки. Теорема о неподвижной точке. Доказательство, примеры. Сжимающее отображение. Определение. Теорема Банаха о неподвижной точке. Доказательство, примеры. Метод Ньютона для решения нелинейных уравнений. Условия сходимости метода. Примеры. |
| Тема 14. | Системы с несколькими первыми интегралами. | Центральная сила. Примеры. Секториальная скорость и доказательство второго закона Кеплера. Эффективная потенциальная энергия. Сохранение энергии радиального движения. Определение фазы. Апоцентр и перицентр. Условие периодичности орбиты. Первый и третий законы Кеплера, Бертрана и Кенига – без док. Сохранение импульса для замкнутой системы. Движение центра масс. Сохранение момента импульса замкнутой системы. Случай сохранения проекции момента импульса в некоторых незамкнутых системах. Сохранение энергии в задаче N-тел. Полная интегрируемость в задаче 2 тел. |
| Тема 15. | Обобщенные функции. | Основные функции (варианты пространства). Пример Коши и разбиение единицы.Топология в пространстве основных функций. Неметризуемость этой топологии.Умножение обобщенной функции на гладкую.Дельта-функция.Обобщенные функции типа функции и другие.Носитель и сингулярный носитель. Примеры.Слабое дифференцирование обобщенных функций. Примеры.Решение ОДУ в пространстве обобщенных функций. Сравнение с классическим решением. Преобразование Фурье обобщенных функций. |
| Тема 16. | Простейшие задачи вариационного исчисления. | Задача согласования информации о координате и скорости. Задача Дидоны. Цепная линия. Катеноид. Брахистохрона. Геодезические. Принцип Ферма и рефракция. Непрерывные и гладкие функционалы. Первая вариация. Необходимое условие экстремума гладкого функционала – равенство нулю первой вариации. Примеры недостаточности этого условия. Вывод уравнения Эйлера. Граничные условия трансверсальности. Условный экстремум и множители Лагранжа. Вторая вариация. Задачи со старшими производными, несколькими функциями и в частных производных. Принцип наименьшего действия. Примеры. |
4. Методические и оценочные материалы
Формы контроля: Контроль знаний студентов включает формы текущего и итогового контроля. Текущий контроль осуществляется в виде коротких контрольных работ в начале многих занятий и контрольной работы в середине триместра. Кроме того, будет выдано несколько домашних работ, которые должны выполняться студентом в течение одной недели. Если она сделана в течение второй недели, оценка за нее делится пополам. После второй недели 10-балльная оценка за сданную работу - нулевая. Итоговый контроль осуществляется в виде двух экзаменов, один из которых теоретический, а второй – обсуждение письменной работы и решение задач на компьютере. Веса обоих экзаменов равные. Итоговая оценка по 100-балльной шкале формируется по формуле Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{О}\text{итог} = 0.3 \times \text{О}\text{предв} + 0.2 \times \text{О}\text{контр} + 0.5 \times \text{О}\text{экз}} . Округление происходит только для итоговой отметки. Кроме того на протяжении курса студентам выдаются домашние задания, где решение требует комбинированного подхода: аналитические соображения + численная компьютерная реализация. Задачи, как правило, содержат индивидуальный параметр Y или параметры.
Задания для практических занятий:
- 1.Доказать, что в некоторой точке на интервале (-1;1) производная функции Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = (1 - x^2)^{100}} равна 1.
- 2.Как повлияет на пропускную способность трубы со стационарным ламинарным течением жидкости а) удвоение перепада давления на концах трубы; б) удвоение диаметра трубы?
- 3.Приведите определение метрического пространства, линейного нормированного пространства, евклидова пространства. Каковы соотношения между этими понятиями?
- 4.Лестница прислоняется к трубе, как показано пунктиром на рисунке. Радиус трубы равен 1. Нижний конец лестницы находится в точке x=1+k/10. Определить координаты точки касания лестницы и трубы. Здесь k – номер студента в списке.
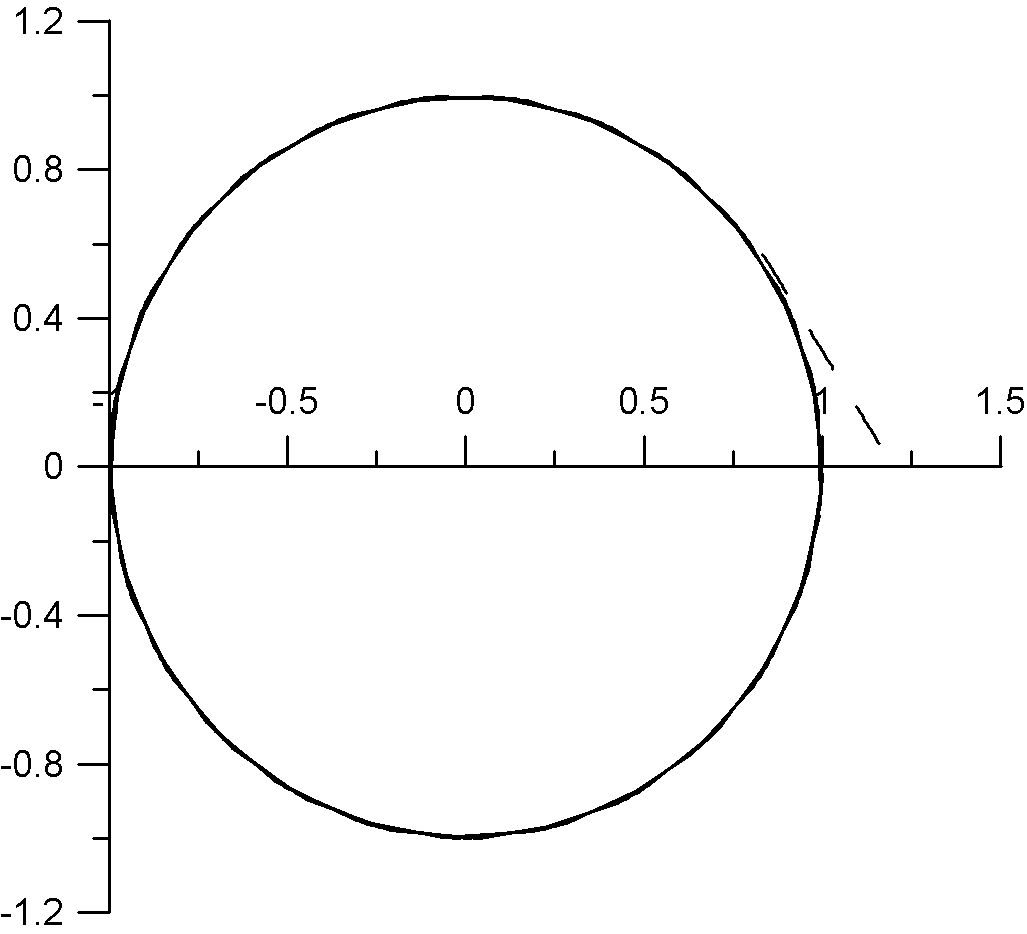
- 5.Из плоскости вырезан круг радиуса 1 с центром в начале координат. Точка A=<1+Y/1000,0> на этой плоскости соединена натянутой нитью с точкой B=<0,1+Y/100>. Определить длину нити. При каком Y нить будет иметь форму отрезка?
- 6.Методом разделения переменных решить уравнениеFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{dx}}{{dt}} = Ax^\alpha} при Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \pm Y} ,α=0,1/2,1,2. Здесь Y – номер студента в списке. Под словом решить понимается описание общего решения при произвольных начальных данных. Для каждого из вариантов построить несколько траекторий.
- 7.Известно, что в момент Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_1 = 7} первая популяция имела численность 2Y, а вторая Y. Первая популяция возрастает со временем согласно уравнению Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{dx}}{{dt}} = Yx} , а вторая Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{dz}}{{dt}} = 2Yz} . В какой момент численности обеих популяций будут (или были) равными?
- 8.Построить график решения уравнения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{dx}}{{dt}} = Yx^2} с начальным условием Y при Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_1 = 0} . В какие моменты решение будет в два раза больше и в два раза меньше начального значения?
- 9.Рассмотрим три дифференциальных уравнения первого порядка вида: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{dz}}{{dt}} = a|z|^b} , где a=2Y,_ b=1-Y/100,_ 1,_ 1+Y/100 с начальным условием при t=0: z(0)=Y. Методом разделения переменных найти решение в максимально возможных пределах в обе стороны по t. Существенен ли знак модуля в уравнении ? Построить графики решений.
- 10.Для уравнения фон Берталанфи с α=1,_ β=Y определить время удвоения объема при различных начальных данных.
- 11.Для уравнения Гомперца финальная масса вдвое больше начальной. Временной масштаб λ=Y. Определить константу r.
- 12.Привести к диагональному виду оператор с матрицей A=

- 13.Решить систему дифференциальных уравнений Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{d\vec{X}}}{{dt}} = A\vec{X}} с упомянутой выше матрицей А и начальным условием X ⃗(0)=<0,0,0,1>. Построить графики компонент решения на отрезке [0,3].
- 14.То же задание для системы с матрицей B=A-2E, E – единичная матрица.
- 15.Ответить еще раз на вопросы 8-10, используя метод Рунге - Кутты. Сравнить полученные графики с аналитическими. Исследовать зависимость погрешности численного решения от шага схемы Р-К и времени интегрирования.
- 16.В шар объемом V вписан цилиндр. При каком радиусе объем цилиндра максимален? При каком радиусе максимальна площадь его поверхности ?
- 17.Чтобы удержать груз на канате, перекинутом через балку, нужна сила ≥10кг, а чтобы начать подтягивать на свою сторону ≥10+ Y кг. Определить вес груза. Определить коэффициент трения, если угол обхвата Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = 10Y} градусов.
- 18.В следующих задачах начальные данные <x,y> для системы двух дифференциальных уравнений первого порядка
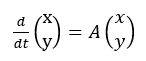 пробегают единичную окружность: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2(0) + y^2(0) = 1}
. Требуется описать (и нарисовать кривые – геометрическое место точек) множество решений в следующие моменты времени t=-1, 1, 2. Для ориентировки: если А – нулевая матрица, то все три искомые кривые совпадают с единичной окружностью, а если А – единичная матрица, то это окружности радиуса e^t. Для каждой задачи указать, имеется ли у системы первый интеграл?
пробегают единичную окружность: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2(0) + y^2(0) = 1}
. Требуется описать (и нарисовать кривые – геометрическое место точек) множество решений в следующие моменты времени t=-1, 1, 2. Для ориентировки: если А – нулевая матрица, то все три искомые кривые совпадают с единичной окружностью, а если А – единичная матрица, то это окружности радиуса e^t. Для каждой задачи указать, имеется ли у системы первый интеграл?
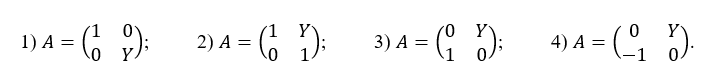
- 19.Для уравнений химической кинетики при Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu = \mu = 1, \quad k1 = 1, \quad k2 = 2} на фазовой области описать множество начальных условий, для которых реакция полностью заканчивается за время Y.
- 20.Пружинный маятник с трением описывается уравнением Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{x} + k\dot{x} + \omega^2x = 0} . Пусть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = 1, \quad k = 2 \pm \frac{Y}{100}} . Построить графики решения при нескольких различных начальных данных. Построить фазовые портреты.
- 21.Длина физического маятника без трения Y см. Ускорение свободного падения g=9,8 м/сек^2. Определить период малых колебаний. Численно определить амплитуду колебаний при которых период вдвое и втрое больше. Для уравнения идеального маятника Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{d^2x}}{{dt^2}} + Y \sin{x} = 0} энергетическим методом построить траектории. Интеграл для периода колебаний вычислить методом Симпсона. Построить график зависимости периода колебаний от его амплитуды.
- 22.Построить методом Рунге – Кутты траектории (несколько - с разными начальными данными) для уравнения маятника с трением Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Y\sin{x} = 0} .
- 23.Тот же вопрос для Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{d^2x}}{{dt^2}} + 11\frac{{dx}}{{dt}} + Y\sin{x} = 0}
- 24.Для уравнения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx = \sin{\omega t}} подобрать частоту Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} так, чтобы амплитуда вынужденных колебаний была максимальна. Построить графики и траектории для решения (с нулевыми начальными условиями) для этой частоты, а также для Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{\omega}}{2}} и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\omega} .
- 25.Построить траектории для уравнения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx^3 = \sin{\omega t}}
- 26.Пусть функция Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi} - ступенчатая, попеременно на отрезках равной длины принимающая значения 1 и -1, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(s) = \text{sign}\sin(s)} .
- 27.Для уравнения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{d^2x}}{{dt^2}} + \frac{{dx}}{{dt}} + Yx = \Psi(\omega t)} подобрать частоту Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} так, чтобы амплитуда вынужденных колебаний была максимальна. Построить графики и траектории для решения (с нулевыми начальными условиями) для этой частоты, а также для Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\omega}{2}} и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\omega} .
- 28.Построить траектории для уравнения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2x}{dt^2} + \frac{dx}{dt} + Yx^3 = \Psi(\omega t)} .
- 29.Определить численно зависимость периода и сдвига фаз между компонентами решения от амплитуды периодических решений системы Лотки – Вольтера при Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = \beta = \gamma = 1, \quad \delta = Y} . Построить графики решений для нескольких вариантов начальных данных.
- 30.Для уравнений химической кинетики построить графики зависимости решения от времени при Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu = 1, \quad \mu = 2, \quad k1 = 10, \quad k2 = Y, \quad n1(0) = 5, \quad n2(0) = 7} .
- 31.Для многочлена Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x) = x^3 + \alpha x^2 + Yx} определить значения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_*} , при которых имеется вырожденная стационарная точка. Как различаются многочлены со значениями Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} по разные стороны от Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_*} ? Построить графики для примеров.
- 32.Параметрическим называется резонанс вследствие изменения коэффициентов уравнения. Для уравнения второго порядка Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'' + x' + Y(1 + a\sin{\omega t})x = 0} численным экспериментом определить, при каких значениях параметров Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a, \omega} теряется устойчивость состояния покоя ? Указать границы областей параметров, где ПР наблюдается. Для нескольких вариантов параметров построить графики решения.
- 33.Пусть каждая пара бессмертных кроликов на первом месяце не рожает, на втором месяце рожает (Y+1) пару, а потом каждый месяц по одной. Найти характеристические числа соответствующего уравнения (график характеристического многочлена построить). Оценить численность популяции спустя много месяцев и сравнить с результатом, полученным прямым вычислением (построить график разности). Вначале была 1 пара, только что родившаяся.
- 34.Для системы уравнений Лотки - Вольтерры с параметрами из задачи 31 определить погрешность (изменение первого интеграла в конечный момент времени по отношению к начальному) в зависимости от периода и шага разностной схемы Рунге - Кутты 4-го порядка с постоянным шагом. Время интегрирования – 100 периодов.
- 35.Использовать экстраполяционный метод Ричардсона для уменьшения этой погрешности. В каком диапазоне шагов метод неэффективен и почему?
- 36.Привести пример линейной системы дифференциальных уравнений с постоянными коэффициентами, для которой начало координат асимптотически устойчиво и существуют решения, модуль которых сначала растет, а потом убывает. Привести графики компонент и модуля таких решений. Возможно ли, чтобы все решения системы с асимптотически устойчивой стационарной точкой обладали таким свойством немонотонности?
- 37.Пусть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x, y) = \sin{x} + \cos{(x + Yy)}} . С помощью леммы Морса исследовать поведение функции в окрестности стационарных (критических) точек. Нарисовать изолинии f.
- 38.ПустьFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x, y, z) = \sin{x} + \cos{(x + Yy)} + \sin{(x + Yy + Y^2z)}} Исследовать поведение функции в окрестности стационарных точек.
- 39.Исследовать системы Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{x} = y \pm Yy^2, \quad \dot{y} = -x \pm x^2} методом разделения переменных. Устойчивы ли стационарные точки этих систем? Сопоставить с исследованием устойчивости методом Ляпунова.
- 40.Для уравнения пружинного маятника с трением Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{x} + \text{sign}(\dot{x}) + Yx = 0} с начальным условием <Y,Y> определить число колебаний до остановки.
- 41. Методом Ньютона исследовать уравнение Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin{z} = Yz, \quad z \in \mathbb{C}}
- 42.Рассмотрим линейный дифференциальный оператор . Докажите, что он оставляет инвариантным подпространство многочленов степени не выше 10. Вычислить матрицу этого оператора в базисе, составленном из этих 11 мономов. Вычислить спектр этого оператора. То же для многочленов степени не выше 12.
- 43.Для дифф. уравнения Бесселя степени 2: построить решение, ограниченное в нуле. При малых r строить разложением в ряд Ньютона, а потом при некотором использовать полученные в качестве начальных данных для метода Рунге - Кутты, каковым интегрировать до 10/\sqrt Y. Оценить зависимость погрешности от числа членов ряда Ньютона, выбора и шага схемы. Применить метод Ричардсона для повышения точности.
- 44.Для сетки {-Y,0,1,2,3} построить многочлен степени 5, который во всех узлах обращается в нуль, а первая производная которого в левой точке равна 1. То же для правой точки. Построить графики.
- 45.На единичной окружности задана равномерная сетка из Y+10 точек. Значения сеточной функции равны значениям функции sin(x). Вычислить в точках сетки первую и вторую производные по компактной схеме и сравнить с истинным результатом. Построить графики.
- 46.На маятник сбоку дует ветер. Поэтому уравнение для его колебаний принимает вид: . Нужно a) Объяснить физический смысл В; b) Построить фазовый портрет и проинтегрировать уравнение при А=1, В=Y. c)При этих же значениях параметров определить зависимость периода от амплитуды и сравнить со случаем В=0.
- 47.Для уравнения маятника с трением рассмотрим решения с начальными данными <1,0> и <0,1>. На фазовой плоскости построить соответствующие параллелограммы при t=-1, 1, 3. Построить график зависимости вронскиана от времени.
- 48. То же для начальных данных в круге . Приложить распечатку программы.
- 49.Для уравнения , зависящего от параметра рассмотрим решения с начальными данными <1,0> и <0,1>. На фазовой плоскости построить для |t|< 1 решения при . Построить разности решений для 0,01 и 0, для 0,02 и 0. Построить решения для уравнения в вариациях, полагая . Для тех же значений . вычислить его решение. Сравнить оба метода. Оценить скорость нарастания погрешности метода уравнения в вариациях со временем.
- 50. Для уравнения второго порядка численным экспериментом определить, в зависимости от значений параметров след и определитель матрицы монодромии. Определите мультипликатор с наибольшим модулем. Постройте кривые, на которых он равен 1, - они являются границами устойчивости нулевого решения (и параметрического резонанса). Сопоставить с результатами задачи, полученными в 53.
- 51.Для уравнения методом вариации постоянных получить общее решение.
- 52.Шарик с нулевой начальной скоростью под действием силы тяжести без трения движется под действием силы тяжести по желобу, имеющему форму параболы, причем z(0)=1, z(Y)=0. Требуется с помощью численных экспериментов определить, какая из парабол обеспечивает наименьшее время для достижения конечной точки.
- 53. Рассмотрим гамильтонову систему с двумя степенями свободы с гамильтонианом
Контрольные вопросы для подготовки к промежуточной аттестации:
- Для оценки качества освоения дисциплины можно использовать задачи, приведенные в задачнике Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. 2008.
- Несколько тысяч задач имеется в тексте книг:
- 1. В.И.Арнольд: Обыкновенные дифференциальные уравнения. М., ``Наука, 1984, 2002.
- 2. В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. М. Издательский Дом ВШЭ. 2016.
- 3. Гордин В.А. Математика, компьютер, прогноз погоды и другие сценарии математической физики. М., ФИЗМАТЛИТ. 2010, 2013.
- 4. Гордин В.А. Прикладная математика. Искусство и ремесло вычислений. Готовится к изданию в М. Издательский Дом ВШЭ. 2024.
Перечень учебно-методического обеспечения дисциплины
Основная литература
- Тема 1.
- В.И.Арнольд: Обыкновенные дифференциальные уравнения. М., ``Наука, 1984, 2002.
- Гельфонд А.О. Исчисление конечных разностей. М., Наука, 1967, УРСС 2012.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., Наука - Физматлит, 1970, Изд. МГУ, 1984. М.: ФИЗМАТЛИТ, 2009, ЛитРес, 2022.
- Тема 2.
- В.И.Арнольд: Обыкновенные дифференциальные уравнения. М., ``Наука, 1984, 2002.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., Наука - Физматлит, 1970, Изд. МГУ, 1984. М.: ФИЗМАТЛИТ, 2009, ЛитРес, 2022.
- Тема 3.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., Наука - Физматлит, 1970, Изд. МГУ, 1984. М.: ФИЗМАТЛИТ, 2009, ЛитРес, 2022.
- Г.М.Фихтенгольц: Курс дифференциального и интегрального исчисления. т. 1. М., Физматгиз, 1963, Лань 2023.
- К.Чен, П.Джиблин, А.Ирвинг: MATLAB в математических исследованиях. М., ``Мир, 2001.
- Тема 4.
- В.И.Арнольд: Обыкновенные дифференциальные уравнения. М., ``Наука, 1984, 2002.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- Оболенский А. Ю. Лекции по качественной теории дифференциальных уравнений — М.; Ижевск, 2006.
- Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., Наука - Физматлит, 1970, Изд. МГУ, 1984. М.: ФИЗМАТЛИТ, 2009, ЛитРес, 2022.
- Тема 5.
- В.И.Арнольд: Обыкновенные дифференциальные уравнения. М., ``Наука, 1984, 2002.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- В.А.Гордин: Математика, компьютер, прогноз погоды и другие сценарии математической физики. М., ФИЗМАТЛИТ, 2010, 2013.
- Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., Наука - Физматлит, 1970, Изд. МГУ, 1984. М.: ФИЗМАТЛИТ, 2009, ЛитРес, 2022.
- Н.М.Матвеев. Методы интегрирования обыкновенных дифференциальных уравнений. М.: Высшая школа, 1967.
- Тема 6.
- В.И. Арнольд, «Жесткие и мягкие математические модели», М., МНЦМО, 2000.
- В.Вольтерра: Математическая теория борьбы за существование.} М., ``Наука", 1976.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- А.А.Самарский, А.П.Михайлов: Математическое моделирование. Физматлит, М., 2002.
- Ю.М.Свирежев, Д.О.Логофет: Устойчивость биологических сообществ. ``Наука, М., 1978.
- Тема 7.
- Гельфонд А.О. Исчисление конечных разностей. М., Наука, 1967, УРСС 2012.
- В.А.Гордин: Как это посчитать? М., МЦНМО, 2005.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- Тема 8.
- Гельфонд А.О. Исчисление конечных разностей. М., Наука, 1967, , УРСС 2012.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- А.А.Андронов, А.А.Витт, С.Э.Хайкин: Теория колебаний, М., Физматгиз, 1959, ``Наука, 1981.
- Зайцев В.Ф., Полянин A.Д. Справочник по нелинейным обыкновенным дифференциальным уравнениям. М., Факториал, 1997.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М., Наука, 1976; Спб. ``Лань, 2003.
- Тема 9.
- Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков: Численные методы. ``Наука, М., 1987.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- Рябенький В.С. Введение в вычислительную математику. М., Наука, 1994, Физматлит, 2008.
- Тема 10.
- Н.М.Матвеев. Методы интегрирования обыкновенных дифференциальных уравнений. М.: Высшая школа, 1967.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- В.А.Гордин: Математика, компьютер, прогноз погоды и другие сценарии математической физики. М., ФИЗМАТЛИТ 2010, 2013.
- Тема 11.
- В.И.Арнольд: Обыкновенные дифференциальные уравнения. М., ``Наука, 1984, 2002.
- В.А.Гордин: Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- Тема 12.
- Айнс Э.Л. Обыкновенные дифференциальные уравнения. Харьков, Государственное научно-техническое издательство Украины, 1939, М. «Факториал Пресс», 2005.
- Федорюк М.В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений. М., Наука, 1983.
- Тема 13.
- Е.Ф.Мищенко, Н.Х.Розов Дифференциальные уравнения с малым параметром и релаксационные колебания. М., Наука, 1975.
- Тема 14.
- В.И.Арнольд. Обыкновенные дифференциальные уравнения. М., ``Наука, 1984, 2002.
- В.А.Гордин. Дифференциальные уравнения. Какие явления они описывают и как их решать. Изд. Дом ВШЭ, М., 2016.
- Л.Д.Ландау, Е.М.Лифшиц. Механика, ``Наука, М., 1965, 1988.
- Тема 15.
- М.С.Агранович. Обобщенные функции. М.: МЦНМО, 2008.
- В.А.Гордин. Математика, компьютер, прогноз погоды и другие сценарии математической физики. М.: Физматлит, 2010; 2013.
- Прикладная математика. Искусство и ремесло вычислений. Готовится к изданию в М. Издательский Дом ВШЭ. 2024.
- Л.Шварц. Математические методы для физических наук. М.: Мир, 1965.
- Г.Е.Шилов. Математический анализ. Второй спецкурс. М.: Наука, 1965.
- Тема 16.
- Буслаев В.С. Вариационное исчисление. Л.: Изд. ЛГУ, 1980.
- И.М.Гельфанд, С.В.Фомин Лекции по вариационному исчислению. М.: Физматгиз, 1961
- В.А.Гордин. Математика, компьютер, прогноз погоды и другие сценарии математической физики. М.: Физматлит, 2010; 2013.
Дополнительная литература
- Тема 1.
- Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М., Мир, 1993.
- Тема 2.
- Абрамовиц М., Стиган И. Справочник по специальным функциям. М., Наука, 1979.
- Шилов Г.Е. Математический анализ. Специальный курс. М., Физматгиз, 1960.
- Тема 3.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М., Наука, 1976; Спб. ``Лань, 2003.
- Зайцев В.Ф., Полянин A.Д. Справочник по нелинейным обыкновенным дифференциальным уравнениям. М., Факториал, 1997.
- Тема 5.
- Айнс Э.Л. Обыкновенные дифференциальные уравнения. Харьков, Государственное научно-техническое издательство Украины, 1939, М. «Факториал Пресс», 2005.
- А.А.Андронов, А.А.Витт, С.Э.Хайкин: Теория колебаний, М., Физматгиз, 1959, ``Наука, 1981.
- В.И.Арнольд, Ю.С.Ильяшенко: Обыкновенные дифференциальные уравнения. В сб. Динамические системы. т.1. Современные проблемы математики. Фундаментальные направления, М., ВИНИТИ, 1985.
- Зайцев В.Ф., Полянин A.Д. Справочник по нелинейным обыкновенным дифференциальным уравнениям. М., Факториал, 1997.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М., Наука, 1976; Спб. ``Лань, 2003.
- Л.Д.Ландау, Е.М.Лифшиц. Механика, ``Наука, М., 1965, 1988.
- Тема 6.
- Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии. М., ФИЗМАТЛИТ, 2010.
- А.С.Братусь, С.В.Дрожжин, Т.С.Якушкина. Математические модели эволюции и динамики репликаторных систем. М., Ленанд, 2022.
- Тема 7.
- Бабенко К.И. Основы численного анализа. М., Наука, 1986, 2002.
- Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М., Мир, 1993.
- Тема 8.
- Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М., Мир, 1993.
- Тема 9.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М., Наука, 1976; Спб. ``Лань, 2003.
- Р.П.Федоренко: Лекции по вычислительной физике. М., МФТИ, 1994, 2008.
- Тема 10.
- Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии. М., ФИЗМАТЛИТ, 2010.
- И.М.Гельфанд. Некоторые задачи теории квазилинейных уравнений. Успехи математических наук, 1959. Т.14. № 2, С.87-158.
- Тема 11.
- Айнс Э.Л. Обыкновенные дифференциальные уравнения. Харьков, Государственное научно-техническое издательство Украины, 1939, М. «Факториал Пресс», 2005.
- В.И.Арнольд: Математические методы классической механики. ``Наука, М., 1989.
- Л.Д.Ландау, Е.М.Лифшиц: Механика, ``Наука, М., 1965, 1988.
- Тема 12.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М., Наука, 1976; СПб.: "Лань, 2003.
- Тема 14.
- А.А.Андронов, А.А.Витт, С.Э.Хайкин: Теория колебаний, М., Физматгиз, 1959, ``Наука, 1981.
- В.И.Арнольд: Математические методы классической механики. ``Наука, М., 1989.
- Тема 16.
- Блисс Г.А. Лекции по вариационному исчислению. М.: Иностранная литература, 1950.
- Лаврентьев М.А., Люстерник Л.А. Курс вариационного исчисления. М.--Л.: ГИТТЛ, 1950.
Методические указания для обучающихся по освоению дисциплины
| Вид учебных занятий/деятельности |
Деятельность обучающегося |
| Лекция | Написание конспекта лекций: кратко, схематично, последовательно фиксировать основные положения лекции, выводы, формулировки, обобщения; помечать важные мысли, выделять ключевые слова, термины. Обозначить вопросы, термины или другой материал, который вызывает трудности, пометить и попытаться найти ответ в рекомендуемой литературе. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия. |
| Практическое (семинарское) занятие | При подготовке к семинарскому (практическому) занятию необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме. На основании обработанной информации постараться сформировать собственное мнение по выносимой на обсуждение тематике. Обосновать его аргументами, сформировать список источников, подкрепляющих его. Во время семинарского (практического) занятия активно участвовать в обсуждении вопросов, высказывать аргументированную точку зрения на проблемные вопросы. Приводить примеры из источниковой базы и научной и/или исследовательской литературы. |
| Устный/письменный опрос | Отвечать, максимально полно, логично и структурировано, на поставленный вопрос. Основная цель – показать всю глубину знаний по конкретной теме или ее части. |
| Подготовка к промежуточной аттестации | При подготовке к промежуточной аттестации необходимо проработать вопросы по темам, которые рекомендуются для самостоятельной подготовки. При возникновении затруднений с ответами следует ориентироваться на конспекты лекций, семинаров, рекомендуемую литературу, материалы электронных и информационных справочных ресурсов, статей. Если тема вызывает затруднение, четко сформулировать проблемный вопрос и задать его преподавателю. |
| Самостоятельная работа | Самостоятельная работа состоит из следующих частей: 1) чтение учебной, справочной, научной литературы; 2) повторение материала лекций; 3) составление планов устных выступлений; 4) подготовка видеопрезентации. При чтении учебной литературы нужно разграничивать для себя материал на отдельные проблемы, концепции, идеи. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис. |
| Контрольная работа | При подготовке к контрольной работе необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. |
| Разработка отдельных частей кода | Разработать часть кода, исходя из поставленной задачи и рекомендаций преподавателя. При выполнении работы рекомендуется обращаться к материалам лекций и семинарских (практических) занятий. Если возникают затруднения, необходимо проконсультироваться с преподавателем. |
| Выполнение домашних заданий и групповых проектов | Для выполнения домашних заданий и групповых проектов необходимо получить формулировку задания от преподавателя и убедиться в понимании задания. При выполнение домашних заданий и групповых проектов необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме. |
Методы и технологии обучения, способствующие формированию компетенции
| Методы и технологии обучения, способствующие формированию компетенции |
|



















