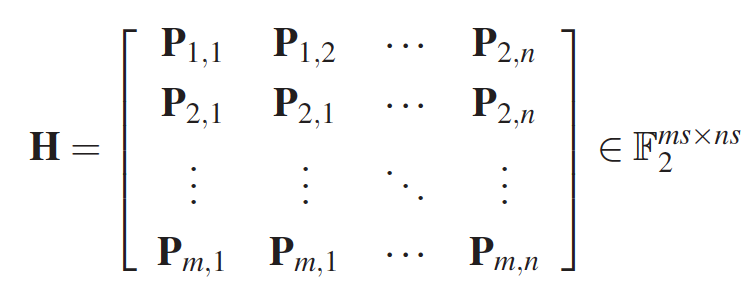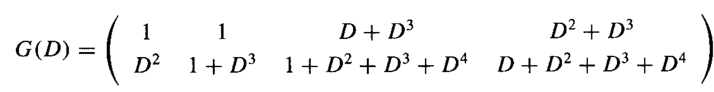Difference between revisions of "BSc: InformationTheory"

From IU
Jump to navigation Jump to search
 
(3 intermediate revisions by the same user not shown)
Line 34: Line 34:
 
| style="text-align:center;" | 1. || Элементы теории информации. || Измерение информации, взаимная информация и энтропия. <br>
  
| style="text-align:center;" | 1. || Элементы теории информации. || Измерение информации, взаимная информация и энтропия. <br>
 
|- style="background-color:#F8F9FA; color:#202122;"
  
|- style="background-color:#F8F9FA; color:#202122;"
−
| style="text-align:center;" | 2. || Кодирование для дискретных источников. || ПТеорема о кодировании источника, префиксные коды, неравенство Крафта, кодирование Хаффмана.<br>
 +
| style="text-align:center;" | 2. || Кодирование для дискретных источников. || Теорема о кодировании источника, префиксные коды, неравенство Крафта, кодирование Хаффмана.<br>
 
Метод типов, универсальное кодирование источника, алгоритм Лемпеля-Зива. <br>
  
Метод типов, универсальное кодирование источника, алгоритм Лемпеля-Зива. <br>
   
Line 133: Line 133:
 
1. Пусть С – это линейным (n, k) код. Докажите следующее утверждение: если С имеет, по меньшей мере, одно кодовое слово нечетного веса, то все кодовые слова четного веса формируют (N, K-1) код.<br>
  
1. Пусть С – это линейным (n, k) код. Докажите следующее утверждение: если С имеет, по меньшей мере, одно кодовое слово нечетного веса, то все кодовые слова четного веса формируют (N, K-1) код.<br>
 
2. Покажите, что любой код длины n = 2k и d = k имеет не более 2n кодовых слов.<br>
  
2. Покажите, что любой код длины n = 2k и d = k имеет не более 2n кодовых слов.<br>
−
3. Пусть С – это линейный код с проверочной матрицей <math> H=[E_{n-k} P], где E_{n-k} </math> обозначает единичную матрицу размера n-k. Найти порождающую матрицу C.<br>
 +
3. Пусть С – это линейный код с проверочной матрицей H=[E_{n-k} P], где E_{n-k} обозначает единичную матрицу размера n-k. Найти порождающую матрицу C.<br>
 
4. Существует ли код с параметрами (15, 12, 3)?<br>
  
4. Существует ли код с параметрами (15, 12, 3)?<br>
   
Line 173: Line 173:
 
2. Докажите, что алгоритм Витерби выполняет декодирование максимального правдоподобия на блок для сверточных кодов. <br>
  
2. Докажите, что алгоритм Витерби выполняет декодирование максимального правдоподобия на блок для сверточных кодов. <br>
 
3. Рассмотрим сверточную матрицу кодирования скорости R = 2/3<br>
  
3. Рассмотрим сверточную матрицу кодирования скорости R = 2/3<br>
−
[[File:5.png|200px|thumb|left|alt text]]
 +
[[File:5.png]]
 
(А) Является ли G(D) основной?<br>
  
(А) Является ли G(D) основной?<br>
 
(Б) Является ли G(D) минимальной?<br>
  
(Б) Является ли G(D) минимальной?<br>
Line 194: Line 194:
 
| style="width:25%" | Форма текущего контроля<br><br>
  
| style="width:25%" | Форма текущего контроля<br><br>
 
| style="width:50%" | Материалы текущего контроля<br><br>
  
| style="width:50%" | Материалы текущего контроля<br><br>
  +
 
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
 
| style="text-align:center;" | 1.
  
| style="text-align:center;" | 1.
  +
| Элементы теории информации<br>
−
| Пределы последовательностей и функций.
  
  +
Кодирование для дискретных источников<br>
−
Отношения порядка и непрерывные функции.
  
  +
Дискретные каналы без памяти<br>
−
| style="text-align:center;" | Устный опрос, Домашние работы, Письменный тест
 
  +
Каналы множественного доступа<br>
−
| В домашние работы включаются задачи, нерешенные во время семинарских занятий.
  
  +
| style="text-align:center;" | Домашняя работа, Коллоквиум
−
Тестирование (письменное или компьютерное):<br>
  
  +
| В домашние работы включаются задачи, нерешенные во время семинарских занятий.<br>
−
1. Две задачи из разделов «Числовые ряды» которые могут быть исследованы с помощью признаков Даламбера и Коши.<br>
 
  +
−
2. Две задачи из раздела «знакопеременные ряды», для решения первой может быть использован признак Лейбница, для второй — теорема Римана о сумме условно сходящегося ряда.
 
 
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
 
| style="text-align:center;" | 2.
  
| style="text-align:center;" | 2.
  +
| Блочные коды<br>
−
| Функциональные ряды: степенные ряды и ряды Фурье.
  
  +
Алгебраические блочные коды<br>
−
| style="text-align:center;" | Домашние работы. Письменный тест.
  
  +
Каскадные коды<br>
−
Устный опрос по темам разделов
  
−
Коллоквиум
+
| style="text-align:center;" | Домашняя работа, Коллоквиум
−
| В домашние работы включаются задачи, нерешенные во время семинарских занятий.
 +
| В домашние работы включаются задачи, нерешенные во время семинарских занятий.<br>
  +
−
Письменный тест содержит пять задач из соответствующих разделов:<br>
  
−
1. Степенные ряды для исследования на сходимость рядов и почленно продифференцированных рядов.<br>
  
−
2. Задачи разложении в ряд Тейлора элементарных функций и комбинаций элементарных функций.<br>
  
−
3. Вычисление коэффициентов рядов Фурье для гладких периодических функций.<br>
  
−
4. Ряды Фурье для четных и нечетных функций.<br>
  
−
5. Вычисление коэффициентов рядов Фурье разрывных функций.
 
 
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
 
| style="text-align:center;" | 3.
  
| style="text-align:center;" | 3.
  +
| Коды на графах<br>
−
| Пределы функций многих переменных, частные производные, градиент. Дифференцируемые многообразия. Экстремумы функций нескольких переменных.
  
  +
Фактор-графы и алгоритм «сумма-произведение»<br>
−
| style="text-align:center;" | Домашние работы. Письменный тест.
  
  +
Построение МПП-кодов<br>
−
Устный опрос по темам разделов
 
  +
| style="text-align:center;" | Домашняя работа, Коллоквиум
−
| В домашние работы включаются задачи, нерешенные во время семинарских занятий. Письменный тест содержит пять задач из соответствующих разделов: предел функции двух переменных; частные производные и производные по направлению; Геометрический смысл частных производных и дифференцируемые многообразия; экстремальные точки и условия максима или минимума; Задачи минимизации на многообразиях — функция Ланранжа.
  
  +
| В домашние работы включаются задачи, нерешенные во время семинарских занятий.<br>
−
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
−
| style="text-align:center;" | 4.
  
−
| Кратные интегралы и Векторный анализ
  
−
| style="text-align:center;" | Домашние работы. Письменный тест.
  
−
Устный опрос по темам разделов
 
−
| В домашние работы включаются задачи, нерешенные во время семинарских занятий. Письменный тест содержит четыре задачи из раздела: Криволинейные интегралы и двумерные интегралы и формула Грина; двумерные и трехмерные интегралы и формула Остроградского-Гаусса; вычисление дивергенции и вычисление ротора для заданных векторных полей.
  
 
|}
  
|}
   
Line 237: Line 228:
 
| style="width:65%" | Вопросы
  
| style="width:65%" | Вопросы
 
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 1. || Элементы теории информации. || Энтропия, совместная энтропия, условная энтропия, относительная энтропия (или дивергенция Кульбака-Лейблера). <br> Взаимная информация, связь с энтропией. Неравенства Йенсена, обработки данных, Фано.
−
| style="text-align:center;" | 1. || Числовые ряды, абсолютно сходящиеся ряды, условно сходящиеся ряды. || 1. Определение сходящегося ряда. Определение ряда, сходящегося абсолютно. Определение ряда, сходящегося условно.<br>
  
−
2. Признаки сходимости Даламбера, Коши, интегральный признак сходимости. Геометрический ряд и его использование как мажорирующего ряда. <br>
  
−
3. Перестановка порядка суммирования в условно сходящемся ряду и приведение его суммы к заранее заданному числу.
  
   
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 2. || Кодирование для дискретных источников. || Уникально декодируемые и префиксные коды. <br>
  +
Неравенство Крафта. <br>
  +
Теорема кодирования источника. <br>
  +
Кодирование Хаффмана. <br>
  +
Универсальное кодирование источника.
   
 
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 3. || Дискретные каналы без памяти. || Каналы передачи с шумом, пропускная способность канала. <br> Прямая и обратная теоремы Шеннона.
−
| style="text-align:center;" | 2. || Функциональные ряды: степенные ряды и ряды Фурье. || 1. Определение интервала сходимости степенного ряда.<br>
  
−
2. Почленное интегрирование и дифференцирование степенных рядов.<br>
  
−
3. Вычисление коэффициентов рядов Фурье. Ряды Фурье для четных и нечетных функций.<br>
  
−
4. Гладкость функций и асимптотические свойства коэффициентов Фурье.
  
   
   
 
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 4. || Каналы множественного доступа. || Канал множественного доступа, широковещательный канал и их пропускные способности.
−
| style="text-align:center;" | 3. || Пределы функций многих переменных, частные производные, градиент. Дифференцируемые многообразия. Экстремумы функций нескольких переменных || 1. Условие существования предела функции нескольких переменных. <br>
  
−
2. Условие перестановки пределов функции нескольких переменных. <br>
  
−
3. Производная по направлению. Градиент. Касательная плоскость. <br>
  
−
4. Дифференцируемое многообразие, карта, атлас. <br>
  
−
5. Необходимое условие экстремума функции нескольких переменных. <br>
  
−
6. Алгоритм определения экстремума функции нескольких переменных на многообразии.
 
   
 
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 5. || Блочные коды. || Минимальное кодовое расстояние (расстояние Хэмминга), декодирование по критерию максимального правдоподобия, декодирование до половины минимального расстояния.<br>
−
| style="text-align:center;" | 4. || Кратные интегралы и Векторный анализ. || 1. Определение и примеры вычисления криволинейных интегралов первого и второго рода. <br>
  
  +
Линейный код, порождающая и проверочная матрицы, синдромное декодирование. Дуальный код, тождества Мак-Вильямс.<br>
−
2. Вывод и примеры использования формулы Грина. <br>
  
  +
Границы для параметров кодов (границы Синглтона, Хэмминга, Плоткина, Элайеса-Бассалыго и Гилберта-Варшамова).<br>
−
3. Вывод и примеры использования формулы Остроградского-Гаусса. <br>
  
  +
Совершенные коды: коды Хэмминга и Голея.
−
4. Определения ротора и дивергенции векторного поля.
 
  +
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 6. || Алгебраические блочные коды. || Коды Рида-Маллера, полиномы Жегалкина, алгоритмы кодирования и декодирования.<br>
  +
Циклические коды, БЧХ коды, алгоритмы декодирования (Берлекемпа-Мэсси, Евклида).<br>
  +
Коды с максимальным достижимым расстоянием (МДР), коды Рида-Соломона.
  +
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 7. || Каскадные коды. || Каскадные коды и их параметры. <br>
  +
Граница Зяблова. <br>
  +
Алгоритм декодирования. <br>
  +
Декодирование по обобщенному минимальному расстоянию.
  +
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 8. || Коды на графах. || Коды LDPC, граф Таннера. <br>
  +
Алгоритмы декодирования с исправлением стираний, алгоритм инвертирования бита и алгоритм Сумма-Произведение. <br>
  +
Графы-расширители, лемма о перемешивании. <br>
  +
Коды Сипсера-Спилмана и Земора. Коды на графах.
  +
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 9. || Фактор-графы и алгоритм «сумма-произведение». || Фактор-граф.<br>
  +
Алгоритмы декодирования «сумма-произведение» и «минимум-сумма».
  +
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 10. || Построение МПП-кодов. || Метод эволюции плотностей.<br>
  +
EXIT диаграммы.<br>
  +
Алгоритмы PEG и ACE.<br>
  +
МПП-коды на основе протографов.<br>
  +
Квазициклические МПП-коды.
  +
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 11. || Элементы сверточных кодов. || Представление в виде дерева, конечного автомата и решетки. <br>
  +
Принцип динамического программирования и алгоритм декодирования Витерби. <br>
  +
Определение и основные свойства. Мягкое декодирование. Свободное расстояние
  +
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 12. || Сверточные МПП-коды. || Построение анализ порога декодирования.
  +
  +
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  +
| style="text-align:center;" | 13. ||Кодирование для распределенных и облачных систем хранения данных. || Восстанавливающие коды.<br>
  +
Коды с локальным восстановлением.<br>
  +
Коды с локальным восстановлением и несколькими восстанавливающими множествами.
  +
 
|}
  
|}
   
 
'''Вопросы/Задания к промежуточной аттестации в устной/письменной форме:'''
  
'''Вопросы/Задания к промежуточной аттестации в устной/письменной форме:'''
   
  +
1.Меры информации. Энтропия, совместная энтропия, условная энтропия, относительная энтропия (или дивергенция Кульбака-Лейблера). Взаимная информация, связь с энтропией. Неравенства Йенсена, обработки данных, Фано.<br>
−
1. Определения абсолютной и условной сходимости ряда и чем они отличаются? Можете ли вы привести пример ряда, который является условно сходящимся, но не абсолютно сходящимся?<br>
  
  +
2.Сжатие данных. Уникально декодируемые и префиксные коды. Неравенство Крафта. Теорема кодирования источника. Кодирование Хаффмана. Универсальное кодирование источника.<br>
−
2. Признаки сходимости Даламбера, Коши, интегральный признак сходимости.<br>
  
  +
3.Зашумленные каналы передачи. Дискретный канал без памяти, симметричный канал. Пропускная способность канала. Теорема Шеннона.<br>
−
3. Геометрический ряд и его использование как мажорирующего ряда.<br>
  
  +
4.Дифференциальная энтропия. Гауссовский канал и его пропускная способность. Параллельные гауссовские каналы.<br>
−
4. Признаки сходимости Абеля и Дирихле. <br>
  
  +
5.Многопользовательские каналы. Канал множественного доступа.<br>
−
5. Перестановка порядка суммирования в условно сходящемся ряду и приведение его суммы к заранее заданному числу.<br>
  
  +
6.Блочные коды. Булев куб как метрическое пространство: расстояние Хэмминга, шар, сфера, слой. Код, минимальное кодовое расстояние. Декодирование по максимуму правдоподобия и декодирование с ограниченным минимальным расстоянием. Обнаружение и исправление ошибок, геометрическая интерпретация.<br>
−
6. Что такое степенной ряд и как определяется его радиус сходимости? Можете ли вы привести пример степенного ряда и его радиуса сходимости?<br>
  
  +
7.Границы параметров кода. Определение A(n,d). Границы Хэмминга, Гилберта, Синглтона и Плоткина. Асимптотический режим.<br>
−
7. Что такое дифференциальное уравнение и как построить степенной ряд для заданного дифференциального уравнения.<br>
  
  +
8.Линейные коды. Определение и основные параметры. Порождающая и проверочная матрицы. Теорема о проверочной матрице линейного кода и ее минимальном расстоянии. Граница Варшамова-Гилберта. Синдром и синдромное декодирования.<br>
−
8. Что такое ряд Фурье и как он используется для аппроксимации периодических функций? Можете ли вы привести пример периодической функции и ее ряда Фурье?<br>
  
  +
9.Дуальный код, нумератор весов и тождества МакВильяма.<br>
−
9. Привести и обосновать формулы для рядов Фурье четных и нечетных функций. Привести примеры.<br>
  
  +
10.Двоичные коды Хэмминга. Совершенные коды. Вычисление синдрома и декодирование кодов Хэмминга.<br>
−
10. Что такое дифференцируемое многообразие и каково его касательное пространство? Можете ли вы привести пример дифференцируемого многообразия и его касательного пространства?<br>
  
  +
11.Коды Рида-Маллера и их параметры. Конструкция Плоткина.<br>
−
11. Что такое градиент функции и как он используется для решения задач оптимизации? Можете ли вы привести пример того, как найти градиент функции и использовать его для решения задачи оптимизации?<br>
  
  +
12.Элементы конечных полей. Группы, кольца, поля. Расширение поля. Поле многочленов. Минимальные полиномы.<br>
−
12. Что такое метод множителя Лагранжа и как он используется для нахождения экстремумов функции на многообразиях? Можете ли вы привести пример того, как использовать этот метод для решения задачи оптимизации?<br>
  
  +
13.Коды МДР и их свойства. Коды Рида-Соломона и дискретное преобразование Фурье. Алгоритм декодирования Петерсона-Горенштейна-Цирлера. Схемы разделения секретов. Схема Шамира.<br>
−
13. Определение двойного интеграла. Суммы Дарбу. Теорема о мере границы.<br>
  
  +
14.Полиномиальные коды. Циклические коды. Эквивалентность полиномиальных и циклических кодов. Порождающие и проверочные многочлены. Несистематическое и систематическое кодирование. Определение циклического кода с использованием корней порождающего полинома.<br>
−
14. Свойства двойных интегралов. Теорема о среднем значении. Примеры.<br>
  
  +
15.Коды БЧХ и их параметры. Коды Рида--Соломона как подкоды кодов БЧХ, алгоритм декодирования Петерсона-Горенштейна-Цирлера.<br>
−
15. Приложения двойного интеграла. Объем, фильтры, масса плоской фигуры, центр масс плоской фигуры. Примеры.<br>
  
  +
16.Каскадные коды и их параметры. Граница Зяблова. Алгоритм декодирования. Декодирование по обобщенному минимальному расстоянию.<br>
−
16. Теорема Фубини, доказательство. Примеры.<br>
  
  +
17.Сверточные коды. Представление в виде дерева, конечного автомата и решетки. Принцип динамического программирования и алгоритм декодирования Витерби. Определение и основные свойства. Мягкое декодирование. Свободное расстояние.<br>
−
17. Геометрический смысл двойных интегралов. Вектор нормали для поверхности. Примеры.<br>
  
  +
18.Коды LDPC, граф Таннера. Алгоритмы декодирования с исправлением стираний, алгоритм инвертирования бита и алгоритм Сумма-Произведение. Графы-расширители, лемма о перемешивании. Коды Сипсера-Спилмана и Земора. Коды на графах.<br>
−
18. Критерии Дарбу для существования меры для данного трехмерного тела. Примеры.<br>
  
  +
19.Фактор-граф. Маргинализация посредством передачи сообщений для деревьев (алгоритм суммы-произведения). Декодирование кодов LDPC посредством передачи сообщений.<br>
−
19. Изменение переменных в двойных интегралах. Якобиан. Полярные координаты в качестве примера.<br>
  
  +
20.Построение кодов LDPC. Нерегулярные коды LDPC. Эволюция плотностей, порог. Множества останова.<br>
−
20. Изменение переменных в тройных интегралах. Якобиан. Примеры.<br>
  
−
21. Сферические координаты и использование сферических координат для вычисления тройных интегралов. Примеры.<br>
  
−
22. Преобразование Фурье. Определение. Набросок доказательства. Примеры.<br>
  
−
23. Свойства преобразования Фурье. Гладкие функции и асимптотическое поведение образа Фурье.<br>
  
−
24. Вычисление двойных интегралов и оценка погрешности.<br>
  
−
25. Плоская кривая. Касательный вектор, вектор нормали, кривизна, длина кривой. Примеры.<br>
  
−
26. Кривая в трехмерном пространстве. Бинормаль, плоскость соприкосновения, кручение. Пример.<br>
  
−
27. Криволинейный интеграл. Работа потенциальной силы вдоль заданной траектории. Центр масс заданной кривой.<br>
  
−
28. Определение скалярного поля и векторного поля. Дивергенция и ротор векторного поля. Примеры.<br>
  
−
29. Формы представления криволинейного интеграла. Примеры использования.<br>
  
−
30. Теорема Гирина. Вывод формулы Грина. Следствие теоремы Грина для кругового интеграла градиента.<br>
  
−
31. Двумерные многообразия. Ориентированные и неориентированные многообразия. Примеры. Локальные карты и атлас. Примеры<br>
  
−
32. Интеграл по поверхности для векторного поля. Различные формы поверхностных интегралов, такие как интеграл по проекциям и интегралы по локальной системе координат. Примеры.<br>
  
−
33. Формула Остроградского-Гаусса. Доказательство формулы. Физическая интерпретация формулы. Примеры.<br>
  
−
34. Ротор и дивергенция как предел циркуляции потока и обтекания поверхности для данного объема. Теорема о расходимости ротора.<br>
  
   
 
=== Перечень учебно-методического обеспечения дисциплины ===
  
=== Перечень учебно-методического обеспечения дисциплины ===
 
Список основной литературы:<br>
  
Список основной литературы:<br>
  +
1. T. M. Cover and J. A. Thomas, Elements of Information Theory. New York: Wiley, 1991<br>
−
1. Кудрявцев, Л. Д. Курс математического анализа в 3 т. Том 1 : учебник для бакалавров / Л. Д. Кудрявцев. — 6-е изд. — Москва : Издательство Юрайт, 2023. — 703 с. — ISBN 978-5-9916-1807-6.<br>
  
  +
2. T. Richardson and R. Urbanke, Modern Coding Theory, Cambridge 2008 (http://ipg.epfl.ch/lib/exe/fetch.php?media=en:publications:mct-new.pdf).<br>
−
2. Фихтенгольц Г. М. Основы математического анализа. Т1. Издательство Лань, 2023, --444 с. -- ISBN 978-5-8114-7583-4, 978-5-8114-5337-5<br>
  
  +
3. Сагалович Ю.Л. Введение в алгебраические коды. М.: ИППИ РАН, 2010. – 302 с.<br>
−
3. Зорич В.А. Математический анализ, Часть 1, Издательство МЦНМО, 2019, --564 с. --ISBN 978-5-4439-4029-8.<br>
  
  +
4. Габидулин Э. М. Лекции по алгебраическому кодированию М. : МФТИ, 2015. – 107 с. <br>
−
4. Демидович Б. П. . Сборник задач и упражнений по математическому анализу: Учебное пособие для вузов Издательство АСТ, 2005. 558 с.<br>
  
   
 
Список дополнительной литературы:<br>
  
Список дополнительной литературы:<br>
  +
1. R. G. Gallager, Information Theory and Reliable Communication. New York: Wiley, 1968.<br>
−
1. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т1. Издательство Интеграл-Пресс, 2002, --416 с. --ISBN 5-89602-012-0<br>
  
  +
2. J. H. van Lint, Introduction to Coding Theory. Springer-Verlag, Berlin, 1999.<br>
−
2. Лутц М., Изучаем Python: Т. 1, Издательство Диалектика, 2023, --824 c. --ISBN 9785521805532<br>
  
  +
3. D. J.C. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press 2003 (http://www.inference.phy.cam.ac.uk/itprnn/book.pdf).<br>
−
3. Beazley D., Jones B.K. Python Cookbook, 3rd Edition by 2013 Publisher(s): O'Reilly Media, Inc.
  
  +
−
ISBN: 9781449357351<br>
  
 
=== Методические указания для обучающихся по освоению дисциплины ===
  
=== Методические указания для обучающихся по освоению дисциплины ===
 
{| class="wikitable" style="width:80%;"
  
{| class="wikitable" style="width:80%;"
Line 372: Line 387:
 
| Методы и технологии обучения, способствующие формированию компетенции
  
| Методы и технологии обучения, способствующие формированию компетенции
 
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
  
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
−
| В курсе планируется использовать несколько технологий обучения. Таких как: <u> интерактивные лекции </u>, поощряющие участие студентов посредством сессий вопросов и ответов, живых демонстраций концепций квантовых вычислений или групповых дискуссий.
 +
| В курсе планируется использовать несколько технологий обучения. Таких как: информационно – коммуникационная технология, педагогика сотрудничества, традиционные технологии, модульная технология.
−  
−
<u> Проблемно-ориентированное обучение </u> – мероприятия по решению проблем, которые побуждают студентов применять концепции квантовых вычислений в практических ситуациях. Этот метод может улучшить навыки критического мышления и закрепления знаний.
  
−  
−
Будут применяться <u> программные библиотеки для аналитических и численных методов: SymPy, NumPy, и SciPy </u>, что позволит использовать компьютер как инструмент для изучения свойств аналитических функции, изучать теорию аппроксимаций и получить опыт использования компьютерных вычислений в задачах математического анализа.
  
−  
−
Планируется предложить <u> совместные проекты </u>, которые требуют применения концепций квантовых вычислений в реальных сценариях или создания новых квантовых алгоритмов. Такой подход может способствовать командной работе, навыкам общения и креативности, одновременно углубляя понимание студентами концепций квантовых вычислений.
  
−  
−
Важный элемент курса – <u> смешанное обучение </u>: сочетание традиционного очного обучения с онлайн-учебными ресурсами, такими как видео, симуляторы или интерактивные викторины. Такой подход может учитывать различные стили обучения и предпочтения, одновременно улучшая понимание учащимися концепций квантовых вычислений.
  
 
&nbsp;
  
&nbsp;
 
|}
  
|}

Latest revision as of 18:49, 4 April 2024

Теория информации

Квалификация выпускника: бакалавр
Направление подготовки: 09.03.01 - “Информатика и вычислительная техника”
Направленность (профиль) образовательной программы: Математические основы ИИ
Программу разработал(а): А.А. Фролов

1. Краткая характеристика дисциплины

Данный курс является вводным курсом по теории информации. В первой части рассматриваются измерение информации, взаимная информация, энтропия, оценка пропускной способности одно- и многопользовательских каналов. Во второй части рассматриваются основы теории кодирования, такие как блочные коды, линейные коды, ограничения на параметры кодов и наиболее популярные алгебраические методы кодирования (коды Хэмминга, Рида-Маллера, БЧХ и Рида-Соломона). Затем рассматриваются современные методы кодирования, т.е. итеративные алгоритмы декодирования и графические модели их представления.

2. Перечень планируемых результатов обучения

Цель освоения дисциплины состоит в том, чтобы объяснить основные идеи и результаты теории информации, некоторые из которых в течение довольно длительного времени используются в науках о данных, в частности, различные энтропийные неравенства, а некоторые появились лишь совсем недавно, например, использование кодов с исправлением ошибок в целях улучшения использования метода k-средних для задач кластеризации.
Задачами дисциплины является изучение основ теории информации для применения полученных знаний в различных задачах машинного обучения.

Общая характеристика результата обучения по дисциплине

Знания:
  • Основы теории информации и измерения информации.
  • Классические алгебраические коды коррекции ошибок и ограничения на параметры кодов.
Умения:
  • Представлять итеративные системы декодирования в виде графических моделей, реализовать эффективные алгоритмы декодирования.
  • Анализировать эффективность изученных схем коррекции ошибок.
Навыки (владения):
  • Владеть навыками работы с научно-исследовательской литературой по теории информации.

3. Структура и содержание дисциплины

№
п/п 		Наименование раздела
дисциплины 		Содержание дисциплины по темам
1. Элементы теории информации. Измерение информации, взаимная информация и энтропия.
2. Кодирование для дискретных источников. Теорема о кодировании источника, префиксные коды, неравенство Крафта, кодирование Хаффмана.

Метод типов, универсальное кодирование источника, алгоритм Лемпеля-Зива.

3. Дискретные каналы без памяти. Каналы передачи с шумом, пропускная способность канала, прямая и обратная теоремы Шеннона.
4. Каналы множественного доступа. Канал множественного доступа, широковещательный канал и их пропускные способности.
5. Блочные коды. Блочные коды коррекции ошибок.

Минимальное кодовое расстояние (расстояние Хэмминга), декодирование по критерию максимального правдоподобия, декодирование до половины минимального расстояния.
Линейный код, порождающая и проверочная матрицы, синдромное декодирование. Дуальный код, тождества Мак-Вильямс.
Границы для параметров кодов (границы Синглтона, Хэмминга, Плоткина, Элайеса-Бассалыго и Гилберта-Варшамова).
Совершенные коды: коды Хэмминга и Голея.

6. Алгебраические блочные коды. Коды Рида-Маллера, полиномы Жегалкина, алгоритмы кодирования и декодирования.

Циклические коды, БЧХ коды, алгоритмы декодирования (Берлекемпа-Мэсси, Евклида).
Коды с максимальным достижимым расстоянием (МДР), коды Рида-Соломона.

7. Каскадные коды. Каскадные, обобщенные каскадные коды.

Многоуровневое кодирование.

8. Коды на графах. МПП-Коды.

Граф Таннера.
Графы-расширители и коды на графах-расширителях.

9. Фактор-графы и алгоритм «сумма-произведение». Фактор-граф.

Алгоритмы декодирования «сумма-произведение» и «минимум-сумма».

10. Построение МПП-кодов. Метод эволюции плотностей.

EXIT диаграммы.
Алгоритмы PEG и ACE.
МПП-коды на основе протографов.
Квазициклические МПП-коды.

11. Элементы сверточных кодов. Решетка (треллис).

Алгоритмы декодирования Витерби и BCJR.
Турбо-коды.

12. Сверточные МПП-коды. Построение анализ порога декодирования.
13. Кодирование для распределенных и облачных систем хранения данных. Восстанавливающие коды.

Коды с локальным восстановлением.
Коды с локальным восстановлением и несколькими восстанавливающими множествами.

4. Методические и оценочные материалы

Задания для практических занятий:

№
п/п 		Наименование раздела
дисциплины (модуля) 		Перечень рассматриваемых тем (вопросов)
1. Элементы теории информации.

1. Какова взаимосвязь между взаимной информацией и энтропией?
2. Может ли средняя взаимная информация быть отрицательной?
3. Выведите цепное правило для энтропии.
4. Каково минимальное значение , при котором р пробегает все множество n-мерных векторов вероятностей?
5. Каково максимальное значение , при котором р пробегает все множество n-мерных векторов вероятностей таким образом, что .

2. Кодирование для дискретных источников. X | = 4 генерирует символы с вероятностями

1. Используйте алгоритм Хаффмана для нахождения оптимального префиксного кода для этого источника.
2. Используйте алгоритм Хаффмана для нахождения другого оптимального префиксного кода с иным набором длин.
3. Найти другой префиксный код, который является оптимальным, но не является результатом использования алгоритма Хаффмана.

3. Дискретные каналы без памяти. 1. Вычислите пропускную способность данного канала

1..png
2. Вычислите пропускную способность данного канала

alt text

где Х представляет собой бинарную переменную, Pr (Z = 0) = Pr (Z = а) = 0,5 и Z не зависит от X. Зависит ли пропускная способность от а?

4. Каналы множественного доступа. 1. Найдите область пропускной способности следующих каналов:

X_1∈{0,1};X_2∈{0,1};Y=X_1+X_2 mod 2
X_1∈{0,1};X_2∈{0,1};Y=X_1*X_2

2. Найдите область пропускной способности деградированного широковещательного канала:

alt text
5. Блочные коды.

1. Пусть С – это линейным (n, k) код. Докажите следующее утверждение: если С имеет, по меньшей мере, одно кодовое слово нечетного веса, то все кодовые слова четного веса формируют (N, K-1) код.
2. Покажите, что любой код длины n = 2k и d = k имеет не более 2n кодовых слов.
3. Пусть С – это линейный код с проверочной матрицей H=[E_{n-k} P], где E_{n-k} обозначает единичную матрицу размера n-k. Найти порождающую матрицу C.
4. Существует ли код с параметрами (15, 12, 3)?

6. Алгебраические блочные коды. 1. Оцените сложность алгоритма декодирования Рида-Маллера.

2. Сравните сложность алгоритмов Берлекемпа-Мэсси и Евклида.
3. Как нужно изменить ключевое уравнение, чтобы исправить и ошибки, и стирания?
4. Найдите проверочную матрицу кода БЧХ длины 15 с конструктивным расстоянием 7 и вычислите ее ранг.
5. Какова минимальная длина регистра, который генерирует последовательность (0 0 0 0 0 0 1)?
6. Какова сложность алгоритма Гурусвами-Судана?

7. Каскадные коды. 1. Как оценить расстояние обобщенного каскадного кода?

2. Каков радиус декодирования каскадного кода, если внутренние и внешние коды декодируются до половины минимального кодового расстояния? Найдите способ улучшения радиуса декодирования.
3. Какова взаимосвязь между обобщенными каскадными кодами и многоуровневым кодированием?
4. Выполните разбиение QAM 64 на 8 классов смежности (максимизируйте минимальное евклидово расстояние).

8. Коды на графах. 1. Как проверить свойство расширения графа?

2. Докажите лемму о перемешивании для расширителя.
3. Каков коэффициент расширения клики〖 K〗_n?
4. Рассмотрим граф Таннера с N символьными узлами и M проверочными узлами. Пусть степени всех символьных узлов равны l, а степени всех проверочных - n_0. Пусть разность между первым и вторым собственными значениями равна λ. Оцените минимальное расстояние кода.

9. Фактор-графы и алгоритм «сумма-произведение». 1. Выведите алгоритм «сумма-произведение» для недвоичных МПП-кодов. Как бы вы представили сообщения в этом случае?

2. Объясните вывод алгоритма «минимум-сумма». Примените декодер «минимум-сумма» для двоичных МПП-кодов. Найдите способ улучшить его корректирующие свойства.

10. Построение МПП-кодов. 1. Предположим, что нам известен протограф и соответствующая матрица инцидентности. Найдите проверочную матрицу МПП-кода на основе протографа.

2. Предположим, что мы имеем проверочную матрицу МПП-кода на основе протографа.

alt text

где P_(i,j) – матрица перестановки размера s. Предложите верхнюю границу на расстояние такого кода.
3. Используя метод эволюции плотностей, найдите оптимальные распределения для скорости 0,2.
4. В чем разница между методом эволюции плотностей и методом EXIT диаграмм?
3. Реализуйте и улучшите алгоритм PEG

11. Элементы сверточных кодов. 1. В чем разница между алгоритмами декодирования Витерби и BCJR?

2. Докажите, что алгоритм Витерби выполняет декодирование максимального правдоподобия на блок для сверточных кодов.
3. Рассмотрим сверточную матрицу кодирования скорости R = 2/3

5.png

(А) Является ли G(D) основной?
(Б) Является ли G(D) минимальной?

12. Сверточные МПП-коды. 1. Написать программу для построения сверточных МПП-кодов.

2. Какова сложность кодирования сверточных МПП-кодов с циклическим замыканием?

13. Кодирование для распределенных и облачных систем хранения данных. 1. Найдите способ построения кода с локальным восстановлением с оптимальной скоростью и двумя восстанавливающими множествами. Докажите его оптимальность.

2. Обычным требованием к кодам с локальным восстановлением является исправление одного стирания с использованием не более r других символов. Найдите способ построения кода, который может исправить любые δ>1 стирания с использованием не более r других символов.

Текущий контроль успеваемости обучающихся по дисциплине:

№
п/п 		Наименование раздела
дисциплины 		Форма текущего контроля

 Материалы текущего контроля

1. Элементы теории информации

Кодирование для дискретных источников
Дискретные каналы без памяти
Каналы множественного доступа

 Домашняя работа, Коллоквиум В домашние работы включаются задачи, нерешенные во время семинарских занятий.
2. Блочные коды

Алгебраические блочные коды
Каскадные коды

 Домашняя работа, Коллоквиум В домашние работы включаются задачи, нерешенные во время семинарских занятий.
3. Коды на графах

Фактор-графы и алгоритм «сумма-произведение»
Построение МПП-кодов

 Домашняя работа, Коллоквиум В домашние работы включаются задачи, нерешенные во время семинарских занятий.

Контрольные вопросы для подготовки к промежуточной аттестации:

№
п/п 		Наименование
раздела дисциплины 		Вопросы
1. Элементы теории информации. Энтропия, совместная энтропия, условная энтропия, относительная энтропия (или дивергенция Кульбака-Лейблера).
Взаимная информация, связь с энтропией. Неравенства Йенсена, обработки данных, Фано.
2. Кодирование для дискретных источников. Уникально декодируемые и префиксные коды.

Неравенство Крафта.
Теорема кодирования источника.
Кодирование Хаффмана.
Универсальное кодирование источника.

3. Дискретные каналы без памяти. Каналы передачи с шумом, пропускная способность канала.
Прямая и обратная теоремы Шеннона.


4. Каналы множественного доступа. Канал множественного доступа, широковещательный канал и их пропускные способности.
5. Блочные коды. Минимальное кодовое расстояние (расстояние Хэмминга), декодирование по критерию максимального правдоподобия, декодирование до половины минимального расстояния.

Линейный код, порождающая и проверочная матрицы, синдромное декодирование. Дуальный код, тождества Мак-Вильямс.
Границы для параметров кодов (границы Синглтона, Хэмминга, Плоткина, Элайеса-Бассалыго и Гилберта-Варшамова).
Совершенные коды: коды Хэмминга и Голея.

6. Алгебраические блочные коды. Коды Рида-Маллера, полиномы Жегалкина, алгоритмы кодирования и декодирования.

Циклические коды, БЧХ коды, алгоритмы декодирования (Берлекемпа-Мэсси, Евклида).
Коды с максимальным достижимым расстоянием (МДР), коды Рида-Соломона.

7. Каскадные коды. Каскадные коды и их параметры.

Граница Зяблова.
Алгоритм декодирования.
Декодирование по обобщенному минимальному расстоянию.

8. Коды на графах. Коды LDPC, граф Таннера.

Алгоритмы декодирования с исправлением стираний, алгоритм инвертирования бита и алгоритм Сумма-Произведение.
Графы-расширители, лемма о перемешивании.
Коды Сипсера-Спилмана и Земора. Коды на графах.

9. Фактор-графы и алгоритм «сумма-произведение». Фактор-граф.

Алгоритмы декодирования «сумма-произведение» и «минимум-сумма».

10. Построение МПП-кодов. Метод эволюции плотностей.

EXIT диаграммы.
Алгоритмы PEG и ACE.
МПП-коды на основе протографов.
Квазициклические МПП-коды.

11. Элементы сверточных кодов. Представление в виде дерева, конечного автомата и решетки.

Принцип динамического программирования и алгоритм декодирования Витерби.
Определение и основные свойства. Мягкое декодирование. Свободное расстояние

12. Сверточные МПП-коды. Построение анализ порога декодирования.
13. Кодирование для распределенных и облачных систем хранения данных. Восстанавливающие коды.

Коды с локальным восстановлением.
Коды с локальным восстановлением и несколькими восстанавливающими множествами.

Вопросы/Задания к промежуточной аттестации в устной/письменной форме:

1.Меры информации. Энтропия, совместная энтропия, условная энтропия, относительная энтропия (или дивергенция Кульбака-Лейблера). Взаимная информация, связь с энтропией. Неравенства Йенсена, обработки данных, Фано.
2.Сжатие данных. Уникально декодируемые и префиксные коды. Неравенство Крафта. Теорема кодирования источника. Кодирование Хаффмана. Универсальное кодирование источника.
3.Зашумленные каналы передачи. Дискретный канал без памяти, симметричный канал. Пропускная способность канала. Теорема Шеннона.
4.Дифференциальная энтропия. Гауссовский канал и его пропускная способность. Параллельные гауссовские каналы.
5.Многопользовательские каналы. Канал множественного доступа.
6.Блочные коды. Булев куб как метрическое пространство: расстояние Хэмминга, шар, сфера, слой. Код, минимальное кодовое расстояние. Декодирование по максимуму правдоподобия и декодирование с ограниченным минимальным расстоянием. Обнаружение и исправление ошибок, геометрическая интерпретация.
7.Границы параметров кода. Определение A(n,d). Границы Хэмминга, Гилберта, Синглтона и Плоткина. Асимптотический режим.
8.Линейные коды. Определение и основные параметры. Порождающая и проверочная матрицы. Теорема о проверочной матрице линейного кода и ее минимальном расстоянии. Граница Варшамова-Гилберта. Синдром и синдромное декодирования.
9.Дуальный код, нумератор весов и тождества МакВильяма.
10.Двоичные коды Хэмминга. Совершенные коды. Вычисление синдрома и декодирование кодов Хэмминга.
11.Коды Рида-Маллера и их параметры. Конструкция Плоткина.
12.Элементы конечных полей. Группы, кольца, поля. Расширение поля. Поле многочленов. Минимальные полиномы.
13.Коды МДР и их свойства. Коды Рида-Соломона и дискретное преобразование Фурье. Алгоритм декодирования Петерсона-Горенштейна-Цирлера. Схемы разделения секретов. Схема Шамира.
14.Полиномиальные коды. Циклические коды. Эквивалентность полиномиальных и циклических кодов. Порождающие и проверочные многочлены. Несистематическое и систематическое кодирование. Определение циклического кода с использованием корней порождающего полинома.
15.Коды БЧХ и их параметры. Коды Рида--Соломона как подкоды кодов БЧХ, алгоритм декодирования Петерсона-Горенштейна-Цирлера.
16.Каскадные коды и их параметры. Граница Зяблова. Алгоритм декодирования. Декодирование по обобщенному минимальному расстоянию.
17.Сверточные коды. Представление в виде дерева, конечного автомата и решетки. Принцип динамического программирования и алгоритм декодирования Витерби. Определение и основные свойства. Мягкое декодирование. Свободное расстояние.
18.Коды LDPC, граф Таннера. Алгоритмы декодирования с исправлением стираний, алгоритм инвертирования бита и алгоритм Сумма-Произведение. Графы-расширители, лемма о перемешивании. Коды Сипсера-Спилмана и Земора. Коды на графах.
19.Фактор-граф. Маргинализация посредством передачи сообщений для деревьев (алгоритм суммы-произведения). Декодирование кодов LDPC посредством передачи сообщений.
20.Построение кодов LDPC. Нерегулярные коды LDPC. Эволюция плотностей, порог. Множества останова.

Перечень учебно-методического обеспечения дисциплины

Список основной литературы:
1. T. M. Cover and J. A. Thomas, Elements of Information Theory. New York: Wiley, 1991
2. T. Richardson and R. Urbanke, Modern Coding Theory, Cambridge 2008 (http://ipg.epfl.ch/lib/exe/fetch.php?media=en:publications:mct-new.pdf).
3. Сагалович Ю.Л. Введение в алгебраические коды. М.: ИППИ РАН, 2010. – 302 с.
4. Габидулин Э. М. Лекции по алгебраическому кодированию М. : МФТИ, 2015. – 107 с.

Список дополнительной литературы:
1. R. G. Gallager, Information Theory and Reliable Communication. New York: Wiley, 1968.
2. J. H. van Lint, Introduction to Coding Theory. Springer-Verlag, Berlin, 1999.
3. D. J.C. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press 2003 (http://www.inference.phy.cam.ac.uk/itprnn/book.pdf).

Методические указания для обучающихся по освоению дисциплины

Вид учебных
занятий/деятельности 		Деятельность обучающегося
Лекция Написание конспекта лекций: кратко, схематично, последовательно фиксировать основные положения лекции, выводы, формулировки, обобщения; помечать важные мысли, выделять ключевые слова, термины. Обозначить вопросы, термины или другой материал, который вызывает трудности, пометить и попытаться найти ответ в рекомендуемой литературе. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия.
Практическое (семинарское) занятие При подготовке к семинарскому (практическому) занятию необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме. На основании обработанной информации постараться сформировать собственное мнение по выносимой на обсуждение тематике. Обосновать его аргументами, сформировать список источников, подкрепляющих его.
Во время семинарского (практического) занятия активно участвовать в обсуждении вопросов, высказывать аргументированную точку зрения на проблемные вопросы. Приводить примеры из источниковой базы и научной и/или исследовательской литературы.
Устный/письменный опрос Отвечать, максимально полно, логично и структурировано, на поставленный вопрос. Основная цель – показать всю глубину знаний по конкретной теме или ее части.
Реферат Поиск источников и литературы, составление библиографии. При написании реферата рекомендуется использовать разнообразные источники, монографии и статьи из научных журналов, позволяющие глубже разобраться в различных точках зрения на заданную тему. Изучение литературы следует начинать с наиболее общих трудов, затем следует переходить к освоению специализированных исследований по выбранной теме. Могут быть использованы ресурсы сети «Интернет» с соответствующими ссылками на использованные сайты.
Если тема содержит проблемный вопрос, следует сформулировать разные точки зрения на него. Рекомендуется в выводах указать свое собственное аргументированное мнение по данной проблеме. Подготовить презентацию для защиты реферата.
Эссе Написание прозаического сочинения небольшого объема и свободной композиции, выражающего индивидуальные впечатления и соображения по конкретному поводу или вопросу и заведомо не претендующего на определяющую или исчерпывающую трактовку предмета. При работе над эссе следует четко и грамотно формулировать мысли, структурировать информацию, использовать основные понятия, выделять причинно-следственные связи. Как правило эссе имеет следующую структуру: вступление, тезис и аргументация его, заключение. В качестве аргументов могут выступать исторические факты, явления общественной жизни, события, жизненные ситуации и жизненный опыт, научные доказательства, ссылки на мнение ученых и др.
Подготовка к промежуточной аттестации При подготовке к промежуточной аттестации необходимо проработать вопросы по темам, которые рекомендуются для самостоятельной подготовки. При возникновении затруднений с ответами следует ориентироваться на конспекты лекций, семинаров, рекомендуемую литературу, материалы электронных и информационных справочных ресурсов, статей.
Если тема вызывает затруднение, четко сформулировать проблемный вопрос и задать его преподавателю.
Практические (лабораторные) занятия Практические занятия предназначены прежде всего для разбора отдельных сложных положений, тренировки аналитических навыков, а также для развития коммуникационных навыков. Поэтому на практических занятиях необходимо участвовать в тех формах обсуждения материала, которые предлагает преподаватель: отвечать на вопросы преподавателя, дополнять ответы других студентов, приводить примеры, задавать вопросы другим выступающим, обсуждать вопросы и выполнять задания в группах. Работа на практических занятиях подразумевает домашнюю подготовку и активную умственную работу на самом занятии. Работа на практических занятиях в форме устного опроса заключается прежде всего в тренировке навыков применять теоретические положения к самому разнообразному материалу. В ходе практических занятий студенты работают в группах для обсуждения предлагаемых вопросов.
Самостоятельная работа Самостоятельная работа состоит из следующих частей: 1) чтение учебной, справочной, научной литературы; 2) повторение материала лекций; 3) составление планов устных выступлений; 4) подготовка видеопрезентации. При чтении учебной литературы нужно разграничивать для себя материал на отдельные проблемы, концепции, идеи. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис.
Видеопрезентация Подготовка видеопрезентаций по курсу. Видеопрезентации могут быть сделаны на любую тему, затронутую в ходе курса. Темы должны быть заранее согласованы с преподавателем. Видеопрезентации продолжительностью около 5 минут (300 секунд) должны быть подготовлены в группах, определяемых преподавателем. Несмотря на то, что это групповая работа, должен явно присутствовать вклад каждого члена группы.
Доклад Публичное, развернутое сообщение по определенной теме или вопросу, основанное на документальных данных. При подготовке доклада рекомендуется использовать разнообразные источники, позволяющие глубже разобраться в теме. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис.
Дискуссия Публичное обсуждение спорного вопроса, проблемы. Каждая сторона должна оппонировать мнение собеседника, аргументируя свою позицию.
Контрольная работа При подготовке к контрольной работе необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме.
Тестирование (устное/письменное) При подготовке к тестированию необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. Основная цель тестирования – показать уровень сформированности знаний по конкретной теме или ее части.
Индивидуальная работа При выполнение индивидуальной работы необходимо взять задание у преподавателя, ознакомиться с требованиями к выполнению работы, изучить поставленную проблему, найти решение проблемы. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия. Оформить результаты работы.
Разработка отдельных частей кода Разработать часть кода, исходя из поставленной задачи и рекомендаций преподавателя. При выполнении работы рекомендуется обращаться к материалам лекций и семинарских (практических) занятий. Если возникают затруднения, необходимо проконсультироваться с преподавателем.
Выполнение домашних заданий и групповых проектов Для выполнения домашних заданий и групповых проектов необходимо получить формулировку задания от преподавателя и убедиться в понимании задания. При выполнение домашних заданий и групповых проектов необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме.

Методы и технологии обучения, способствующие формированию компетенции

Методы и технологии обучения, способствующие формированию компетенции
В курсе планируется использовать несколько технологий обучения. Таких как: информационно – коммуникационная технология, педагогика сотрудничества, традиционные технологии, модульная технология.

 

Retrieved from "https://eduwiki.innopolis.university/index.php?title=BSc:_InformationTheory&oldid=9372"