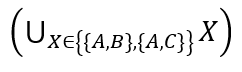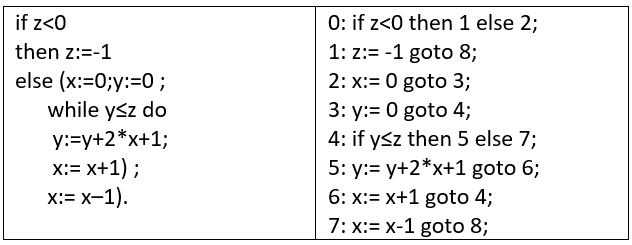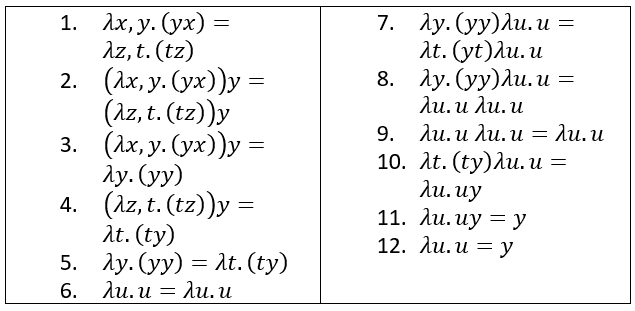Latest revision as of 20:35, 2 April 2024

Математическая логика для ИИ (углубленный курс)

Квалификация выпускника: бакалавр

Направление подготовки: 09.03.01 - “Информатика и вычислительная техника”

Направленность (профиль) образовательной программы: Математические основы ИИ

Программу разработал(а): Николай Вячеславович Шилов, к.ф.-м.н., доцент Университета Иннополис

1. Краткая характеристика дисциплины

Этот элективный курс предназначен для студентов, изучающих искусственный интеллект информатику и математику, чтобы подготовить для и к работе с формальной семантикой, спецификацией и верификацией систем искусственного интеллекта посредством изучения формальной семантики, спецификаций и верификацией программы. Мы начнем с упрощенного подхода к формальной семантике, основанного на игрушечном языке с эзотерической операционной, денотационной и логической (аксиоматической) семантикой. Затем мы переходим к операционной, денотационной и аксиоматической семантике простого императивного языка программирования. Заканчивается курс реферативной работой студентов с современными статьями по формальной семантике, спецификации и верификации систем искусственного интеллекта.

2. Перечень планируемых результатов обучения

Целью освоения дисциплины является подготовка будущих специалистов в области математики и искусственного интеллекта для и к работе с формальной семантикой, спецификацией и верификацией систем искусственного интеллекта посредством изучения формальной семантики, спецификаций и верификацией программы.

Задачами дисциплины являются освоение понятий операционной, денотационной и логической (аксиоматической) семантики программ и систем, а так же знакомство с современным использованием формальной семантики, спецификации и верификации в разработке надежных и безопасных систем искусственного интеллекта.

Общая характеристика результата обучения по дисциплине

Знания: по окончанию курса у студентов будут сформированы систематические знания зачем нужна формальная семантика программ и систем, понятие операционного, денотационного и аксиоматического подходов к формальной семантике, как использовать формальную семантику для анализа и формальной верификации программ и систем (в том числе – искусственного интеллекта).

Умения: по окончанию курса студенты будут уметь определить операционную, дотациональную и аксиоматическую семантику для простого языка программирования, формально задавать и верифицировать вручную простые вычислительные программы на простом языке программирования, выделять и формально специфицировать свойства систем искусственного интеллекта.

Навыки (владения): по окончанию курса студенты будут иметь навыки работы и использования формальной семантики для анализа и формальной верификации реальных программ и систем, внедрения формальной семантики, спецификации и верификации в практику разработки систем искусственного интеллекта.

3. Структура и содержание дисциплины

№ п/п	Наименование раздела дисциплины	Содержание дисциплины по темам
1.	Резюме необходимых знаний по дискретно математике, наивной теории множеств и классической логике.	Обзорные лекции и тест по дискретной математике, наивной теории множеств, логике высказываний. Основы алгебры бинарных отношений, обзор логики предикатов первого порядка, понятие парадигм программирования.
2.	Введение в формальные семантики.	Что такое семантика? Зачем нужна формальная семантика программы? Понятие операционной, денотационной и аксиоматической семантики (на примере эзотерического языка «программирования»).
3.	Формальная семантика простого императивного языка программирования.	Типы данных и их семантика. Основной ингредиент: семантика реализации. Структурная операционная семантика (SOS). Реляционная денотатационная семантика. Аксиоматическая семантика. Элементы дедуктивной верификации программ.
4.	λ-исчисление и классическая денотационная семантика.	Синтаксис, семантика и основные свойства λ-исчисления. Денотационная семантика простого императивного языка программирования.
5.	На пути к спецификации и верификации систем искусственного интеллекта.	Коллоквиум со студенческими рефератами актуальных (5-6) работ по формальной спецификации и верификации систем искусственного интеллекта. .

4. Методические и оценочные материалы

Задания для практических занятий:

№ п/п	Наименование раздела дисциплины (модуля)	Перечень рассматриваемых тем (вопросов)
1.	Резюме необходимых знаний по дискретно математике, наивной теории множеств и классической логике.	Обзорные лекции и тест по дискретной математике, наивной теории множеств, логике высказываний. Основы алгебры бинарных отношений, основ теории формальных языков, обзор логики предикатов первого порядка, понятие парадигм программирования.
2.	Введение в формальные семантики.	Что такое семантика? Зачем нужна формальная семантика программы? Понятие операционной, денотационной и аксиоматической семантики (на примере эзотерического языка «программирования»).
3.	Формальная семантика простого императивного языка программирования.	Типы данных и их семантика. Основной ингредиент: семантика реализации. Структурная операционная семантика (SOS). Реляционная денотатационная семантика. Аксиоматическая семантика. Элементы дедуктивной верификации программ.
4.	λ-исчисление и классическая денотационная семантика.	Синтаксис, семантика и основные свойства λ-исчисления. Денотационная семантика простого императивного языка программирования.
5.	На пути к спецификации и верификации систем искусственного интеллекта.	Коллоквиум со студенческими рефератами актуальных (5-6) работ по формальной спецификации и верификации систем искусственного интеллекта.

Текущий контроль успеваемости обучающихся по дисциплине:

№ п/п	Наименование раздела дисциплины	Форма текущего контроля	Материалы текущего контроля
1.	Резюме необходимых знаний по дискретно математике, наивной теории множеств и классической логике.	Проверка домашнего задания с устным опросом.	1.Пусть A, B и C – конечные множества. Докажите (не используя аксиому множества всех подмножеств), что $(2^{A,B,C})$ – тоже множество. Докажите (не используя аксиому объединения подмножеств), что – тоже множество. 2.Докажите (используя аксиому экстенсиональности) Единственность пустого множества. Единственность множества $\left\{A_{1},\dots A_{n}\right\}$ для каждого явно заданой совокупности множеств $A_{1},\dots A_{n}$ , 3.Докажите (используя аксиому конечного перечисления и объединения множеств) существование объединения двух множеств (A∪B). 4.Докажите (используя аксиому конечного перечисления и объединения множеств) существование пересечения двух множеств (A∩B). 5.Докажите, что для любых множества A и его подмножества B дополнение – тоже множество. 6.Докажите (методом от противного и с использованием аксиомы выделения что так называемое «множество всех множеств» не является множеством (Парадокс Рассела).
2.	Введение в формальные семантики.	Проверка домашнего задания с устным опросом.	1.Охарактеризуйте в терминах иерархии Хомского учебный язык TEL. 2.Охарактеризуйте в терминах иерархии Хомского диалект учебного языка TEL, в котором добавлены структурные правила отступов как языке Python. 3.Предположим, что все переменные в учебном языке TEL имеют целый тип, а сами программы имеют общепринятую «программистскую семантику». Какую функцию тогда вычисляет следующая программа: ? 4.Покажите, что min⁡ $\left\{1,1+1+0+1\right\}$ является операционной семантикой программы в рамках учебного языка TEL. 5.Докажите, что в рамках учебного языка TEL программы α и (α) эквивалентны. 6.Докажите, что в рамках учебного языка TEL программы if-then-else и while-do не эквивалентны.
3.	Формальная семантика простого императивного языка программирования.	Проверка домашнего задания с устным опросом.	1.Является ли учебный язык ToyPL-VM контекстно-свободным? Есть ли у этого языка контекстно-свободный синтаксис? 2.Предположим, что все переменные в учебном языке ToyPL-VM имеют целый тип, а сами программы имеют общепринятую «программистскую семантику». Какую функцию тогда вычисляет следующая программа (ответ доказать): 0: if z<0 then 1 else 2; 1: z:= -1 goto 8; 2: x:= 0 goto 3; 3: y:= 0 goto 4; 4: if y≤z then 5 else 7; 5: y:= y+2*x+1 goto 6; 6: x:= x+1 goto 4; 7: x:= x-1 goto 8; 3. Пусть S – программа на учебном языке ToyPL-VM pro, s – ее произвольное состояние. Определите индукцией по структуре произвольного терма t его значение s(t) в этом состоянии. 4. Докажите, что реализационная семантика программы на учебном языке ToyPL из левой колонки задается программой на учебном языке ToyPL-VM из правой колонки. 5. Выберете все тождественно истинные тройки из перечисленных ниже. (Объясните выбор!)
4.	λ-исчисление и классическая денотационная семантика.	Проверка домашнего задания с устным опросом.	1.Какой из перечисленных ниже λ-термов на самом деле приставляет «терм» λy.xy(λx.xy)? a. ((λy.(xy))((λx.x)y)) b. (λy.((xy)(λx.(xy)))) c. (λy.((xy)(λx.(xy)))) d. (((λy.x)y)(λx.(xy))) e. (((λy.x)y)((λx.x)y)) 2.Перечислите все свободные и связанные вхождения переменных в λ-термы (a)-(e) из предыдущего вопроса. Какие из перечисленных λ-терминов являются комбинаторами? 3.Объясните следующее «доказательство» и почему доказанное равенство приводит к противоречию: 4. Предложите какой-либо другой комбинатор неподвижной точки вместо Y≡λf.((λx.(f(xx)))(λx.(f(xx)))). 5. Приведите пример λ-терма, граф редукций которого a. состоит из одной вершины и одного ребра; b. является цепью дины n; c. является бесконечной цепью.
5.	На пути к спецификации и верификации систем искусственного интеллекта.	Проверка домашнего задания с устным опросом.	Список актуальных статей спецификации и верификации систем искусственного интеллекта будет определен на момент чтения курса (из опубликованных не позже, чем за 2 предыдущие года).

Контрольные вопросы для подготовки к промежуточной аттестации:

№ п/п	Наименование раздела дисциплины	Вопросы
1.	Резюме необходимых знаний по дискретно математике, наивной теории множеств и классической логике.	Что такое наивной теории множеств? Что такое логика высказываний? Основы алгебры бинарных отношений, основ теории формальных языков, обзор логики предикатов первого порядка, понятие парадигм программирования..
2.	Введение в формальные семантики.	Что такое семантика? Зачем нужна формальная семантика программы? Понятие операционной, денотационной и аксиоматической семантики (на примере эзотерического языка «программирования»).
3.	Формальная семантика простого императивного языка программирования.	Типы данных и их семантика. Основной ингредиент: семантика реализации. Структурная операционная семантика (SOS). Реляционная денотатационная семантика. Аксиоматическая семантика. Элементы дедуктивной верификации программ.
4.	λ-исчисление и классическая денотационная семантика.	Синтаксис, семантика и основные свойства λ-исчисления. Денотационная семантика простого императивного языка программирования.

Вопросы/Задания к промежуточной аттестации в устной/письменной форме:

1. Using definition of the natural number as in the lecture notes for section 1, construct the powerset for a given (specified) natural number n. How many elements does it (the powerset) contains? (Explain all your answers.)
2. Using definitions from the lecture notes for section 2, construct a TEL “meaningful program” that after evaluation according to TEL informal semantics gets value month, construct (step by step) its operational, denotational, and axiomatic semantics according to the TEL definitions. Here “meaningful” means that you can explain what does the program computes assuming a conventional informal program semantics. Please explain informally what this semantics is.
3. Using definitions from the lecture notes for section 3, and the same program as you construct in the exercise 2 above, construct (step by step) its operational and denotational semantics as a ToyPL program.
4. Using definitions from the lecture notes for section 3, and the same program as you construct in the exercise 2 above, specify the program by pre- and post-conditions according to your explanations (in the exercise 2) of what does the program compute, and then verify (using Floyd method or Hoare axiomatic semantics) correctness of the specified program.
5. Using definitions from the lecture notes for section 4, construct a given (specified) natural number n. Whether it is a combinator? Build reduction graph for λx.(x True){n}. (Explain all your answers.)
7. Let us assume that ‘∅’, ‘{‘, ‘}’, and ‘,’ are symbols. Using definition of the natural number as in the lecture notes on the topic 1, count (ignoring blank spaces) the length of the string thar represents a given natural number n . How many elements does this representation contains? (Explain all your answers.)
8. Using definitions from the lecture notes on the topic 2, construct a TEL-program that in conventional (natural for a programming language) semantics computes (outputs) the integer part of the square root of a (input) positive integer, but that after evaluation according to TEL informal semantics gets value (n+1) for a given natural number n, construct (step by step) its operational, denotational, and axiomatic semantics according to the TEL definitions.
9. Using definitions from the lecture notes on the topic 3, and the same program as you construct in the exercise 2 above, construct (step by step) its implementation and denotational semantics as a ToyPL program.
10. Using definitions from the lecture notes on the topic 3, and the same program as you construct in the exercise 2 above, specify the program by pre- and post-conditions according to your explanations (in the exercise 2) of what does the program compute, and then verify (using Floyd method or Hoare axiomatic semantics) correctness of the specified program.
11. Using definitions from the lecture notes on the topics 4 and 5, construct explicitly the numeral {n+1} for a given natural number n. What is type of the numeral {n+1}? Demonstrate that {n+1}=Suc{n+1}. What is type of the term λx.(x True){n+1}? Build reduction graph for λx.(x True){n+1}. (Explain all your answers.)

Перечень учебно-методического обеспечения дисциплины

Список основной литературы:

Х. Барендрегт: Ламбда-исчисление. Его синтаксис и семантика. М.: Мир, 1985.
Н.В. Шилов: Ведение в синтаксис, семантику и верификацию программ. Новосибирск: Новосибирский государственный университет, 2011.

Список дополнительной литературы:

Э.В. Дейкстра: Дисциплина программирования. М.: Мир, 1978.
Д. Грис: Наука программирования. М. : Мир, 1984.
Wasilewska: Logics for Computer Science. Classical and Non-Classical. Springer Cham. 2018.
Список 5-6 актуальных статей спецификации и верификации систем искусственного интеллекта будет определен на момент чтения курса (из опубликованных не позже, чем за 2 предыдущие года).

Методические указания для обучающихся по освоению дисциплины

Вид учебных занятий/деятельности	Деятельность обучающегося
Лекция	Написание конспекта лекций: кратко, схематично, последовательно фиксировать основные положения лекции, выводы, формулировки, обобщения; помечать важные мысли, выделять ключевые слова, термины. Обозначить вопросы, термины или другой материал, который вызывает трудности, пометить и попытаться найти ответ в рекомендуемой литературе. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия.
Практическое (семинарское) занятие	При подготовке к семинарскому (практическому) занятию необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме. На основании обработанной информации постараться сформировать собственное мнение по выносимой на обсуждение тематике. Обосновать его аргументами, сформировать список источников, подкрепляющих его. Во время семинарского (практического) занятия активно участвовать в обсуждении вопросов, высказывать аргументированную точку зрения на проблемные вопросы. Приводить примеры из источниковой базы и научной и/или исследовательской литературы.
Устный/письменный опрос	Отвечать, максимально полно, логично и структурировано, на поставленный вопрос. Основная цель – показать всю глубину знаний по конкретной теме или ее части.
Реферат	Поиск источников и литературы, составление библиографии. При написании реферата рекомендуется использовать разнообразные источники, монографии и статьи из научных журналов, позволяющие глубже разобраться в различных точках зрения на заданную тему. Изучение литературы следует начинать с наиболее общих трудов, затем следует переходить к освоению специализированных исследований по выбранной теме. Могут быть использованы ресурсы сети «Интернет» с соответствующими ссылками на использованные сайты. Если тема содержит проблемный вопрос, следует сформулировать разные точки зрения на него. Рекомендуется в выводах указать свое собственное аргументированное мнение по данной проблеме. Подготовить презентацию для защиты реферата.
Эссе	Написание прозаического сочинения небольшого объема и свободной композиции, выражающего индивидуальные впечатления и соображения по конкретному поводу или вопросу и заведомо не претендующего на определяющую или исчерпывающую трактовку предмета. При работе над эссе следует четко и грамотно формулировать мысли, структурировать информацию, использовать основные понятия, выделять причинно-следственные связи. Как правило эссе имеет следующую структуру: вступление, тезис и аргументация его, заключение. В качестве аргументов могут выступать исторические факты, явления общественной жизни, события, жизненные ситуации и жизненный опыт, научные доказательства, ссылки на мнение ученых и др.
Подготовка к промежуточной аттестации	При подготовке к промежуточной аттестации необходимо проработать вопросы по темам, которые рекомендуются для самостоятельной подготовки. При возникновении затруднений с ответами следует ориентироваться на конспекты лекций, семинаров, рекомендуемую литературу, материалы электронных и информационных справочных ресурсов, статей. Если тема вызывает затруднение, четко сформулировать проблемный вопрос и задать его преподавателю.
Практические (лабораторные) занятия	Практические занятия предназначены прежде всего для разбора отдельных сложных положений, тренировки аналитических навыков, а также для развития коммуникационных навыков. Поэтому на практических занятиях необходимо участвовать в тех формах обсуждения материала, которые предлагает преподаватель: отвечать на вопросы преподавателя, дополнять ответы других студентов, приводить примеры, задавать вопросы другим выступающим, обсуждать вопросы и выполнять задания в группах. Работа на практических занятиях подразумевает домашнюю подготовку и активную умственную работу на самом занятии. Работа на практических занятиях в форме устного опроса заключается прежде всего в тренировке навыков применять теоретические положения к самому разнообразному материалу. В ходе практических занятий студенты работают в группах для обсуждения предлагаемых вопросов.
Самостоятельная работа	Самостоятельная работа состоит из следующих частей: 1) чтение учебной, справочной, научной литературы; 2) повторение материала лекций; 3) составление планов устных выступлений; 4) подготовка видеопрезентации. При чтении учебной литературы нужно разграничивать для себя материал на отдельные проблемы, концепции, идеи. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис.
Видеопрезентация	Подготовка видеопрезентаций по курсу. Видеопрезентации могут быть сделаны на любую тему, затронутую в ходе курса. Темы должны быть заранее согласованы с преподавателем. Видеопрезентации продолжительностью около 5 минут (300 секунд) должны быть подготовлены в группах, определяемых преподавателем. Несмотря на то, что это групповая работа, должен явно присутствовать вклад каждого члена группы.
Доклад	Публичное, развернутое сообщение по определенной теме или вопросу, основанное на документальных данных. При подготовке доклада рекомендуется использовать разнообразные источники, позволяющие глубже разобраться в теме. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис.
Дискуссия	Публичное обсуждение спорного вопроса, проблемы. Каждая сторона должна оппонировать мнение собеседника, аргументируя свою позицию.
Контрольная работа	При подготовке к контрольной работе необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме.
Тестирование (устное/письменное)	При подготовке к тестированию необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. Основная цель тестирования – показать уровень сформированности знаний по конкретной теме или ее части.
Индивидуальная работа	При выполнение индивидуальной работы необходимо взять задание у преподавателя, ознакомиться с требованиями к выполнению работы, изучить поставленную проблему, найти решение проблемы. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия. Оформить результаты работы.
Разработка отдельных частей кода	Разработать часть кода, исходя из поставленной задачи и рекомендаций преподавателя. При выполнении работы рекомендуется обращаться к материалам лекций и семинарских (практических) занятий. Если возникают затруднения, необходимо проконсультироваться с преподавателем.
Выполнение домашних заданий и групповых проектов	Для выполнения домашних заданий и групповых проектов необходимо получить формулировку задания от преподавателя и убедиться в понимании задания. При выполнение домашних заданий и групповых проектов необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме.

Методы и технологии обучения, способствующие формированию компетенции

Методы и технологии обучения, способствующие формированию компетенции
Традиционные технологии (классно-урочная система).

@@ Line 90: / Line 90: @@
 | style="text-align:center;" | Проверка домашнего задания с устным опросом.
 |
-#Пусть A, B и C – конечные множества.
+.Пусть A, B и C – конечные множества. <br>
-*Докажите (не используя аксиому множества всех подмножеств), что  <math>(2^{A,B,C})</math> – тоже множество.
+*Докажите (не используя аксиому множества всех подмножеств), что  <math>(2^{A,B,C})</math> – тоже множество.<br>
-*Докажите (не используя аксиому объединения подмножеств), что [[File:n1.png|100px|thumb|left|alt text]] – тоже множество.
+*Докажите (не используя аксиому объединения подмножеств), что [[File:n1.png|200px]] – тоже множество. <br>
-#Докажите (используя аксиому экстенсиональности)
+.Докажите (используя аксиому экстенсиональности) <br>
-*Единственность пустого множества.
+*Единственность пустого множества.<br>
 *Единственность множества <math>\left\{A_1,\dots A_n\right\}</math> для каждого явно заданой совокупности множеств <math>A_1,\dots A_n</math>,<br>
-#Докажите (используя аксиому конечного перечисления и объединения множеств) существование объединения двух множеств <math>(A∪B). </math>,<br>
+.Докажите (используя аксиому конечного перечисления и объединения множеств) существование объединения двух множеств (A∪B). <br>
-#Докажите (используя аксиому конечного перечисления и объединения множеств) существование пересечения двух множеств <math>(A∩B).</math>,<br>
+.Докажите (используя аксиому конечного перечисления и объединения множеств) существование пересечения двух множеств (A∩B).<br>
-#Докажите, что для любых множества A и его подмножества B дополнение <math>(¬B)={x:x∈A но x∉B }</math> – тоже множество.
+.Докажите, что для любых множества A и его подмножества B дополнение [[File:n2.png|250px]] – тоже множество. <br>
-#Докажите (методом от противного и с использованием аксиомы выделения что так называемое «множество всех множеств» не является множеством  (Парадокс Рассела).
+.Докажите (методом от противного и с использованием аксиомы выделения что так называемое «множество всех множеств» не является множеством  (Парадокс Рассела).<br>
-.<br>
 |- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
 | style="text-align:center;" | 2.
+| Введение в формальные семантики.
-| Расходящиеся ряды.
-| style="text-align:center;" | Разработка кода для иллюстрации теоретических положений раздела.
+| style="text-align:center;" | Проверка домашнего задания с устным опросом.
+|
-| Выбрать одну из задач для практических заданий и написать  программу для решений такой задачи.<br>
+.Охарактеризуйте в терминах иерархии Хомского учебный язык TEL. <br>
+.Охарактеризуйте в терминах иерархии Хомского диалект учебного языка TEL, в котором добавлены структурные правила отступов как языке Python.<br>
+.Предположим, что все переменные в учебном языке TEL имеют целый тип, а сами программы имеют общепринятую «программистскую семантику». Какую функцию тогда вычисляет следующая программа: [[File:n3.png|350px]]?<br>
+.Покажите, что min⁡ <math>\left\{1, 1+1+0+1\right\}</math> является операционной семантикой программы [[File:n4.png|350px]] в рамках учебного языка TEL.<br>
+.Докажите, что в рамках учебного языка TEL программы α и  (α) эквивалентны.<br>
+.Докажите, что в рамках учебного языка TEL программы if-then-else и while-do не эквивалентны.<br>
+<br>
 |- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
 | style="text-align:center;" | 3.
+| Формальная семантика простого императивного языка программирования.
-| Анализ на многообразиях нецелой размерности.
-| style="text-align:center;" | Разработка кода для иллюстрации теоретических положений раздела.
+| style="text-align:center;" | Проверка домашнего задания с устным опросом.
+|
-| Выбрать одну из задач для практических заданий и написать  программу для решений такой задачи.<br>
+.Является ли учебный язык ToyPL-VM контекстно-свободным? Есть ли у этого языка контекстно-свободный синтаксис? <br>
+.Предположим, что все переменные в учебном языке ToyPL-VM имеют целый тип, а сами программы имеют общепринятую «программистскую семантику». Какую функцию тогда вычисляет следующая программа (ответ доказать):<br>
+: if z<0 then 1 else 2; <br>
+: z:= -1 goto 8; <br>
+: x:= 0 goto 3; <br>
+: y:= 0 goto 4; <br>
+: if y≤z then 5 else 7; <br>
+: y:= y+2*x+1 goto 6; <br>
+: x:= x+1 goto 4; <br>
+: x:= x-1 goto 8;<br>
+. Пусть S – программа на учебном языке ToyPL-VM pro, s – ее произвольное состояние. Определите индукцией по структуре произвольного терма t его значение s(t) в этом состоянии.<br>
+. Докажите, что реализационная семантика программы на учебном языке ToyPL из левой колонки задается программой на учебном языке ToyPL-VM из правой колонки. <br>
+[[File:n5.png|450px]]
+. Выберете все тождественно истинные тройки из перечисленных ниже. (Объясните выбор!) <br>
+[[File:n6.png|450px]]
+|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
+| style="text-align:center;" | 4.
+| λ-исчисление и классическая денотационная семантика.
+| style="text-align:center;" | Проверка домашнего задания с устным опросом.
+|
+.Какой из перечисленных ниже λ-термов на самом деле приставляет «терм» λy.xy(λx.xy)?<br>
+a.  ((λy.(xy))((λx.x)y))<br>
+b.  (λy.((xy)(λx.(xy))))<br>
+c.  (λy.((xy)(λx.(xy))))<br>
+d.  (((λy.x)y)(λx.(xy)))<br>
+e.  (((λy.x)y)((λx.x)y))<br>
+.Перечислите все свободные и связанные вхождения переменных в λ-термы (a)-(e) из предыдущего вопроса. Какие из перечисленных λ-терминов являются комбинаторами?<br>
+.Объясните следующее «доказательство» и почему доказанное равенство приводит к противоречию:<br>
+[[File:n7.png|450px]]<br>
+.	Предложите какой-либо другой комбинатор неподвижной точки вместо  <br>
+	Y≡λf.((λx.(f(xx)))(λx.(f(xx)))).<br>
+. Приведите пример λ-терма, граф редукций которого <br>
+a.  состоит из одной вершины и одного ребра;<br>
+b.  является цепью дины n;<br>
+c.  является бесконечной цепью.<br>
+|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
+| style="text-align:center;" | 5.
+| На пути к спецификации и верификации систем искусственного интеллекта.
+| style="text-align:center;" | Проверка домашнего задания с устным опросом.
+| Список актуальных статей спецификации и верификации систем искусственного интеллекта будет определен на момент чтения курса (из опубликованных не позже, чем за 2 предыдущие года).
 |}
@@ Line 123: / Line 171: @@
 | style="width:65%" | Вопросы
 |-  style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
-| style="text-align:center;" | 1. || Элементы теории аппроксимации. ||
+| style="text-align:center;" | 1. || Резюме необходимых знаний по дискретно математике, наивной теории множеств и классической логике. ||
+Что такое наивной теории множеств? Что такое логика высказываний? Основы алгебры бинарных отношений, основ теории формальных языков, обзор логики предикатов первого порядка, понятие парадигм программирования..<br>
-#Определение суммирования по Чезаро.  Привести пример расходящегося ряда, суммируемого по Чезаро.<br>
-#Определение суммирования по Борелю. Привести пример ряда, суммируемого по Борелю, но расходящегося по Чезаро.<br>
-#Дать определение асимптотического ряда.<br>
-#Дать определение калибровочной последовательности.<br>
 |- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
-| style="text-align:center;" | 2. || Расходящиеся ряды. ||
+| style="text-align:center;" | 2. || Введение в формальные семантики. ||
+Что такое семантика? Зачем нужна формальная семантика программы? Понятие операционной, денотационной и аксиоматической семантики (на примере эзотерического языка «программирования»).<br>
-#Определение суммирования по Чезаро.  Привести пример расходящегося ряда, суммируемого по Чезаро.<br>
-#Определение суммирования по Борелю. Привести пример ряда, суммируемого по Борелю, но расходящегося по Чезаро.<br>
-#Дать определение асимптотического ряда.<br>
-#Дать определение калибровочной последовательности.<br>
 |- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
-| style="text-align:center;" | 3. || Анализ на многообразиях нецелой размерности.||
+| style="text-align:center;" | 3. || Формальная семантика простого императивного языка программирования.||
+Типы данных и их семантика. Основной ингредиент: семантика реализации. Структурная операционная семантика (SOS). Реляционная денотатационная семантика. Аксиоматическая семантика. Элементы дедуктивной верификации программ.<br>
-#Дать определение фрактальной размерности. Привести примеры многообразий нецелой размерности.<br>
-#Привести примеры отображений, генерирующих многообразия фрактальной размерности.<br>
-#Определение интеграла  Дробного порядка и производной дробного порядка.<br>
+|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
+| style="text-align:center;" | 4. || λ-исчисление и классическая денотационная семантика.||
+Синтаксис, семантика и основные свойства λ-исчисления.  Денотационная семантика простого императивного языка программирования.<br>
 |}
 '''Вопросы/Задания к промежуточной аттестации в устной/письменной форме:'''
+. Using definition of the natural number as in the lecture notes for section 1, construct the powerset for a given (specified) natural number n. How many elements does it (the powerset) contains? (Explain all your answers.)<br>
-#Плотность множества рациональных чисел и мера множества рациональных чисел на интервале (0,1).<br>
+. Using definitions from the lecture notes for section 2, construct a TEL “meaningful program” that after evaluation according to TEL informal semantics gets value month, construct (step by step) its operational, denotational, and axiomatic semantics according to the TEL definitions. Here “meaningful” means that you can explain what does the program computes assuming a conventional informal program semantics. Please explain informally what this semantics is. <br>
-#Теорема Лиувилля о приближении алгебраических чисел рациональными.<br>
+. Using definitions from the lecture notes for section 3, and the same program as you construct in the exercise 2 above, construct (step by step) its operational and denotational semantics as a ToyPL program.<br>
-#Теорема о существовании трансцендентных чисел. Интерполяционный полином Лагранжа и явление Рунге.<br>
+. Using definitions from the lecture notes for section 3, and the same program as you construct in the exercise 2 above, specify the program by pre- and post-conditions according to your explanations (in the exercise 2) of what does the program compute, and then verify (using Floyd method or Hoare axiomatic semantics) correctness of the specified program.<br>
-#Аппроксимация функции частичной суммой ряда Фурье.  Явление Гиббса.<br>
+. Using definitions from the lecture notes for section 4, construct a given (specified) natural number n. Whether it is a combinator? Build reduction graph for λx.(x True){n}. (Explain all your answers.)<br>
-#Аппроксимация функции заданной в узлах Чебышева.<br>
+. Let us assume that ‘∅’, ‘{‘, ‘}’, and ‘,’ are symbols. Using definition of the natural number as in the lecture notes on the topic 1, count (ignoring blank spaces) the length of the string thar represents a given natural number n . How many elements does this representation contains? (Explain all your answers.)<br>
-#Сплайны, дефект сплайна, кривые Безье. Приложения.<br>
+. Using definitions from the lecture notes on the topic 2, construct a TEL-program that in conventional (natural for a programming language) semantics computes (outputs) the integer part of the square root of a (input) positive integer, but that after evaluation according to TEL informal semantics gets value (n+1) for a given natural number n, construct (step by step) its operational, denotational, and axiomatic semantics according to the TEL definitions. <br>
-#Определение Паде аппроксимации заданного порядка. Построение Паде аппроксимации для произвольной гладкой функции.<br>
+. Using definitions from the lecture notes on the topic 3, and the same program as you construct in the exercise 2 above, construct (step by step) its implementation and denotational semantics as a ToyPL program.<br>
-#Сходимость Паде аппроксимации.<br>
+. Using definitions from the lecture notes on the topic 3, and the same program as you construct in the exercise 2 above, specify the program by pre- and post-conditions according to your explanations (in the exercise 2) of what does the program compute, and then verify (using Floyd method or Hoare axiomatic semantics) correctness of the specified program.<br>
-#Примеры расходящихся рядов.<br>
+. Using definitions from the lecture notes on the topics 4 and 5, construct explicitly the numeral {n+1} for a given natural number n. What is type of the numeral {n+1}? Demonstrate that {n+1}=Suc{n+1}. What is type of the term λx.(x True){n+1}? Build reduction graph for λx.(x True){n+1}. (Explain all your answers.) <br>
-#Ряды суммируемые по Чезаро.<br>
-#Суммирование по Борелю.<br>
-#Приложения рядов, суммируемых по Борелю.<br>
-#Калибровочная последовательность. Определение, примеры.<br>
-#Асимптотические ряды. Определение асимптотического ряда. Свойства асимптотических рядов. Интегрирование и дифференцирование асимптотических рядов.<br>
-#Теорема о единственности асимптотического разложения.<br>
-#Приложения асимптотических рядов.<br>
-#Примеры фракталов.<br>
-#Определение хаусдорфовой размерности.<br>
-#Примеры отображений, приводящих к фрактальным многообразиям.<br>
-#Алгоритм вычисления размерности. Фрактальная производная.<br>
-#Определение интеграла дробной размерности.<br>
-#Производные дробной размерности. Примеры <br>
 === Перечень учебно-методического обеспечения дисциплины ===
 Список основной литературы:<br>
+*Х. Барендрегт: Ламбда-исчисление. Его синтаксис и семантика. М.: Мир, 1985. <br>
-#А.Б. Шидловский. Трансцендентные числа. Наука, 1987, 448 с.<br>
+*Н.В. Шилов: Ведение в синтаксис, семантику и верификацию программ. Новосибирск: Новосибирский государственный университет, 2011.<br>
-#Н.Н. Калиткин. Численные методы. Литрес, 2015, 587 с.<br>
-#Р. Эдвардс, Ряды Фурье в современном изложении. Мир, 1985, т1, 264 с.<br>
-#Дж. Бейкр мл. П. Грейвс-Моррис. Аппроксимации Паде, Москва «Мир»1986, 496 с.<br>
-#А.М. Ильин, А.Р. Данилин. Асимптотические методы в анализе. Физматлит, 2009, 248 с.<br>
-#Г. Харди, Расходящиеся ряды. Ленанд, 2022, 504 с.<br>
-#Морозов А.Д., Введение в теорию фракталов, Ижевск, Институт компьютерных исследований, 2002, 160 с.<br>
-#С.Г. Самко, А.А. Килбас, О.И. Маричев Интгералы и производные дробного порядка и некоторые их приложения. Минск, Наука и техника, 1987, 688 с.<br>
 Список дополнительной литературы:<br>
+*Э.В. Дейкстра: Дисциплина программирования.  М.: Мир, 1978.<br>
-#Glebov S.G., Kiselev O.M., Tarkhanov N., Nonlinear equations with small parameter. Volume I: Oscillations and resonances  De Gruyter Series in Nonlinear Analysis and Applications. 2017, v. 23/1, pp.340.<br>
+*Д. Грис: Наука программирования. М. : Мир, 1984.<br>
-#Лутц М., Изучаем Python: Т. 1, 2,   Издательство  Диалектика, 2023, ISBN 9785521805532<br>
+*Wasilewska: Logics for Computer Science. Classical and Non-Classical. Springer Cham. 2018.<br>
-#Beazley D., Jones B.K.  Python Cookbook, 3rd Edition by 2013 Publisher(s): O'Reilly Media, Inc. ISBN: 9781449357351<br>
+*Список 5-6 актуальных статей спецификации и верификации систем искусственного интеллекта будет определен на момент чтения курса (из опубликованных не позже, чем за 2 предыдущие года).<br>
 === Методические указания для обучающихся по освоению дисциплины ===
@@ Line 245: / Line 272: @@
 | Методы и технологии обучения, способствующие формированию компетенции
 |- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;"
+| Традиционные технологии (классно-урочная система).
-| В курсе  планируется использовать несколько технологий обучения. Таких как: <u> интерактивные лекции </u>, поощряющие участие студентов посредством сессий вопросов и ответов, живых демонстраций концепций квантовых вычислений или групповых дискуссий.
-<u> Проблемно-ориентированное обучение </u> – мероприятия по решению проблем, которые побуждают студентов применять концепции квантовых вычислений в практических ситуациях. Этот метод может улучшить навыки критического мышления и закрепления знаний.
-Будут применяться <u> программные библиотеки для аналитических и численных методов: SymPy, NumPy, и SciPy </u>, что позволит использовать компьютер как инструмент для изучения свойств аналитических функции,  изучать теорию аппроксимаций и получить опыт использования компьютерных вычислений в задачах математического анализа.
-Планируется предложить <u> совместные проекты </u>, которые требуют применения концепций квантовых вычислений в реальных сценариях или создания новых квантовых алгоритмов. Такой подход может способствовать командной работе, навыкам общения и креативности, одновременно углубляя понимание студентами концепций квантовых вычислений.
-Важный элемент курса –  <u> смешанное обучение </u>: сочетание традиционного очного обучения с онлайн-учебными ресурсами, такими как видео, симуляторы или интерактивные викторины. Такой подход может учитывать различные стили обучения и предпочтения, одновременно улучшая понимание учащимися концепций квантовых вычислений.
 &nbsp;
 |}

Difference between revisions of "BSc: MathematicalLogicForAiADV"