Difference between revisions of "BSc: TheoreticalMechanics"
V.matiukhin (talk | contribs) |
V.matiukhin (talk | contribs) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 89: | Line 89: | ||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| style="text-align:center;" | 1. ||Предмет кинематики. Кинематика точки и простейших движений твёрдых тел.|| |
| style="text-align:center;" | 1. ||Предмет кинематики. Кинематика точки и простейших движений твёрдых тел.|| |
||
| − | + | 1. Уравнения движения точки имеют вид:<br> |
|
| − | x = 2 cos( |
+ | <math>x = 2 cos(\pi t^2/ 6) + 1</math><br> |
| − | y = 2 sin( |
+ | <math>y = 2 sin(\pi t^2/ 6) - 3</math><br> |
Найти траекторию движения точки, а также для момента времени 1 с определить скорость точки, полное касательное и нормальное ускорения точки, радиус кривизны траектории.<br> |
Найти траекторию движения точки, а также для момента времени 1 с определить скорость точки, полное касательное и нормальное ускорения точки, радиус кривизны траектории.<br> |
||
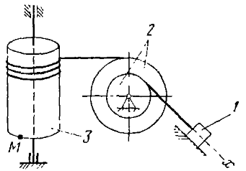
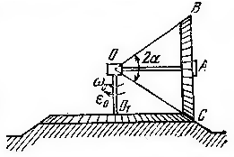
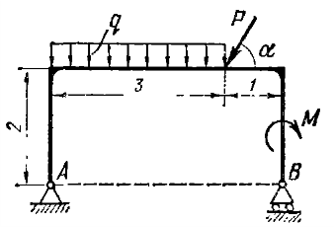
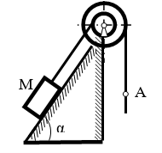
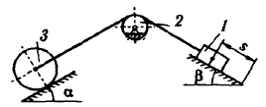
| − | + | 2. Задана механическая система (см. рис).Все геометрические параметры системы известны. Груз 1 движется по закону <math>x = 0,1+0,2t^2</math>(м).<br> |
|
| − | Найти законы вращения колёс, их угловые скорости и ускорения, а |
+ | Найти законы вращения колёс, их угловые скорости и ускорения, а также определить скорость и ускорение точки М в момент времени, когда груз пройдёт расстояние 0,15 м.<br> |
[[File:w1.png]] |
[[File:w1.png]] |
||
| Line 107: | Line 107: | ||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| style="text-align:center;" | 3. ||Сферическое движение. Общий случай движения твёрдого тела.|| |
| style="text-align:center;" | 3. ||Сферическое движение. Общий случай движения твёрдого тела.|| |
||
| − | Коническое зубчатое колесо, свободно насаженное на кривошип |
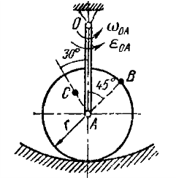
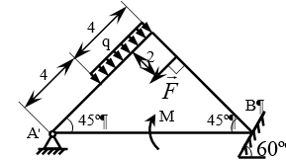
+ | Коническое зубчатое колесо, свободно насаженное на кривошип <math>OA</math>, обкатывается по основанию (см. рис). Считая что известны все геометрические параметры системы, угловая скорость и угловое ускорение кривошипа, определить угловую скорость и угловое ускорение колеса, скорости и ускорения точек <math>B</math> и <math>C</math>.<br> |
[[File:w6.png]]<br> |
[[File:w6.png]]<br> |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| style="text-align:center;" | 4. ||Сложное движение.|| |
| style="text-align:center;" | 4. ||Сложное движение.|| |
||
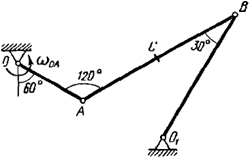
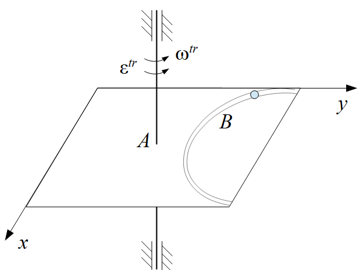
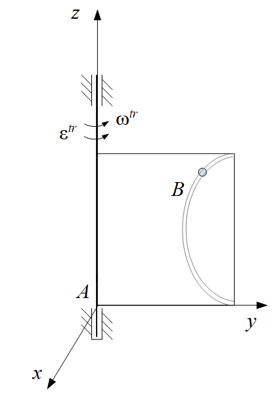
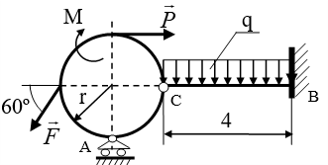
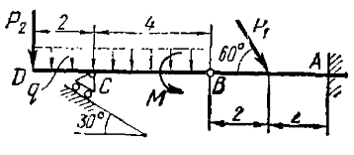
| − | Дана рамка (варианты 1 и 2), вращающаяся вокруг вертикальной оси. В рамке |
+ | Дана рамка (варианты 1 и 2), вращающаяся вокруг вертикальной оси. В рамке выполнен канал, по которому движется точка <math>B</math>. Считая, что задан относительный закон движения и все геометрические параметры системы, определить скорость и ускорение точки относительно неподвижного наблюдателя в заданный момент времени.<br> |
[[File:w7.png]]<br> |
[[File:w7.png]]<br> |
||
[[File:w8.png]]<br> |
[[File:w8.png]]<br> |
||
| Line 128: | Line 128: | ||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| style="text-align:center;" | 7. ||Предмет динамики. Динамика материальной точки.|| |
| style="text-align:center;" | 7. ||Предмет динамики. Динамика материальной точки.|| |
||
| − | Тело массой m движется в вертикальной плоскости из положения А с начальной скоростью |
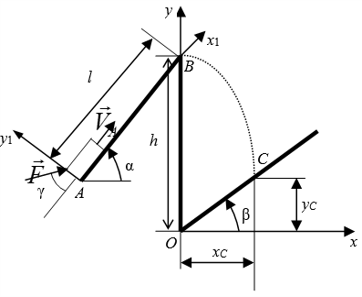
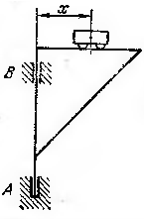
+ | Тело массой <math>m</math> движется в вертикальной плоскости из положения А с начальной скоростью <math>V_A</math> (см. рис. 1). На участке <math>AB</math> длиной <math>l</math> движение происходит по шероховатой плоскости (коэффициент трения скольжения <math>f</math>). На этом участке на точку действует постоянная сила <math>F</math>. В положения <math>B</math> точка покидает плоскость и движется только под действием силы тяжести без учета сопротивления воздуха.<br> |
Требуется:<br> |
Требуется:<br> |
||
| − | 1. Получить уравнение движения точки на участках |
+ | 1. Получить уравнение движения точки на участках <math>AB</math> и <math>BC</math><br> |
| − | 2. Найти время движения точки на участках |
+ | 2. Найти время движения точки на участках <math>AB</math> и <math>BC</math>.<br> |
| − | 3. Определить координаты и скорость точки в положении |
+ | 3. Определить координаты и скорость точки в положении <math>C</math>.<br> |
[[File:w14.png]]<br> |
[[File:w14.png]]<br> |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
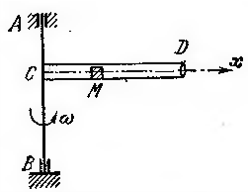
| − | | style="text-align:center;" | 8. ||Динамика относительного движения материальной точки.|| Трубка равномерно вращается с угловой скоростью ω, в трубке движется тело М. Пренебрегая трением и считая известными все геометрические |
+ | | style="text-align:center;" | 8. ||Динамика относительного движения материальной точки.|| Трубка равномерно вращается с угловой скоростью ω, в трубке движется тело М. Пренебрегая трением и считая известными все геометрические парамеnры системы и начальные условия, определить скорость тела в момент вылета из трубки и время движения тела до вылета.<br> |
[[File:w15.png]]<br> |
[[File:w15.png]]<br> |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| style="text-align:center;" | 9. ||Теоремы о движении центра масс и количества движения.|| |
| style="text-align:center;" | 9. ||Теоремы о движении центра масс и количества движения.|| |
||
| − | 1. Лодка покоится на озере. Человек перемещается с одного конца лодки на другой. Считая |
+ | 1. Лодка покоится на озере. Человек перемещается с одного конца лодки на другой. Считая изdестными все массово-геометрические параметры системы и пренебрегая силами сопротивления определить на какое расстояние переместится лодка.<br> |
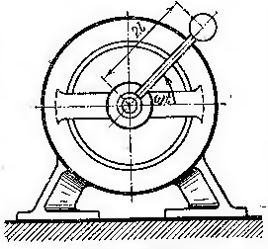
2. Электродвигатель установлен на гладкой горизонтальной поверхности. На валу мотора закреплён стержень с грузом на конце. Вал мотора вращается с постоянной угловой скоростью. Считая, что все массово-геометрические параметры системы известны, определить:<br> |
2. Электродвигатель установлен на гладкой горизонтальной поверхности. На валу мотора закреплён стержень с грузом на конце. Вал мотора вращается с постоянной угловой скоростью. Считая, что все массово-геометрические параметры системы известны, определить:<br> |
||
::1) горизонтальное перемещение мотора при отсутствии креплений; |
::1) горизонтальное перемещение мотора при отсутствии креплений; |
||
| Line 147: | Line 147: | ||
::3) угловую скорость вращения вала, при которой мотор начнёт “подпрыгивать” над опорой.<br> |
::3) угловую скорость вращения вала, при которой мотор начнёт “подпрыгивать” над опорой.<br> |
||
[[File:w16.png]]<br> |
[[File:w16.png]]<br> |
||
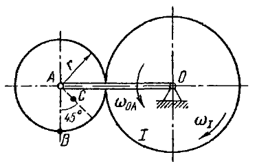
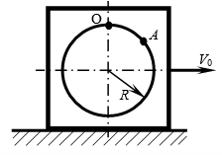
| − | 3. Квадратная пластина массой m движется по гладкой горизонтальной плоскости со скоростью |
+ | 3. Квадратная пластина массой m движется по гладкой горизонтальной плоскости со скоростью <math>V_0 = 5</math> м/c. В некоторый момент времени по кольцевому каналу радиуса <math>R = 0,6</math> м из положения <math>O</math> начинает двигаться точка <math>A</math> массой <math>0,2m</math> с постоянной скоростью <math>V_r=2</math> м/с.<br> |
| − | Определить скорость пластины, когда точка пройдёт расстояние S= |
+ | Определить скорость пластины, когда точка пройдёт расстояние <math>S=OA=9\pi</math> м.<br> |
[[File:w17.png]]<br> |
[[File:w17.png]]<br> |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| style="text-align:center;" | 10. ||Теорема об изменении кинетического момента.|| |
| style="text-align:center;" | 10. ||Теорема об изменении кинетического момента.|| |
||
| − | 1. Груз М весом |
+ | 1. Груз М весом <math>P</math> удерживается на наклонной плоскости человеком весом <math>Q</math>, ухватившимся за веревку в точке <math>A</math>. Затем человек стал подниматься по веревке вверх со скоростью u относительно веревки. Считая, что все массово-геометрические параметры системы известны, и пренебрегая весом блока и трением, определить скорость движения груза <math>M</math>.<br> |
[[File:w18.png]]<br> |
[[File:w18.png]]<br> |
||
2. Имеется полноповоротный кран, с установленной на нём тележкой. Все массово-геометрические параметры системы известны.<br> |
2. Имеется полноповоротный кран, с установленной на нём тележкой. Все массово-геометрические параметры системы известны.<br> |
||
| Line 159: | Line 159: | ||
::*определить закон изменения угловой скорости крана при неподвижной тележке, считая, что кран приводится во вращение постоянным моментом и пренебрегая силами сопротивления;<br> |
::*определить закон изменения угловой скорости крана при неподвижной тележке, считая, что кран приводится во вращение постоянным моментом и пренебрегая силами сопротивления;<br> |
||
::*определить закон изменения угловой скорости крана, считая, что тележка движется с постоянной скоростью по стреле крана, а кран приводится во вращение постоянным моментом и пренебрегая силами сопротивления;<br> |
::*определить закон изменения угловой скорости крана, считая, что тележка движется с постоянной скоростью по стреле крана, а кран приводится во вращение постоянным моментом и пренебрегая силами сопротивления;<br> |
||
| − | ::*определить закон изменения угловой скорости крана, считая, что тележка движется с постоянной скоростью по стреле крана, а кран приводится во вращение постоянным моментом равным |
+ | ::*определить закон изменения угловой скорости крана, считая, что тележка движется с постоянной скоростью по стреле крана, а кран приводится во вращение постоянным моментом равным <math>M_0 - \alpha \omega</math>, где <math>M0</math> и <math>\alpha</math> - заданные константы, а <math>\omega</math> - угловая скорость вращения крана.<br> |
[[File:w19.png]]<br> |
[[File:w19.png]]<br> |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
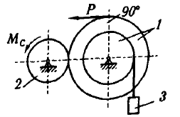
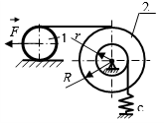
| − | | style="text-align:center;" | 11. ||Дифференциальные уравнения движения твёрдого тела и системы твёрдых тел.||Для заданной механической системы, считая, что все активные силы и все массово- |
+ | | style="text-align:center;" | 11. ||Дифференциальные уравнения движения твёрдого тела и системы твёрдых тел.||Для заданной механической системы, считая, что все активные силы и все массово-геометрические параметры известны, определить закон движения груза 3 и силы взаимодействия между телами системы.<br> |
[[File:w20.png]]<br> |
[[File:w20.png]]<br> |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
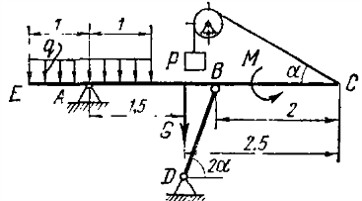
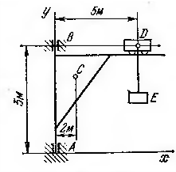
| style="text-align:center;" | 12. ||Метод кинетостатики.||Считая, что все активные силы и все массово-геометрические параметры известны, определить реакции в опорах крана:<br> |
| style="text-align:center;" | 12. ||Метод кинетостатики.||Считая, что все активные силы и все массово-геометрические параметры известны, определить реакции в опорах крана:<br> |
||
| − | - при поднимании груза E с ускорением 0,3g;<br> |
+ | - при поднимании груза <math>E</math> с ускорением <math>0,3g</math>;<br> |
| − | - при движении тележки D с ускорением 0,5g при отсутствии груза E.<br> |
+ | - при движении тележки <math>D</math> с ускорением <math>0,5g</math> при отсутствии груза <math>E</math>.<br> |
[[File:w21.png]]<br> |
[[File:w21.png]]<br> |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| style="text-align:center;" | 13. ||Теорема об изменении кинетической энергии материальной точки.|| |
| style="text-align:center;" | 13. ||Теорема об изменении кинетической энергии материальной точки.|| |
||
| − | Механическая система начинает движение из состояния покоя под действием силы тяжести груза 1. Определить скорость груза 1 как функцию пройденного грузом |
+ | Механическая система начинает движение из состояния покоя под действием силы тяжести груза 1. Определить скорость груза 1 как функцию пройденного грузом пути <math>S</math>.<br> |
[[File:w22.png]]<br> |
[[File:w22.png]]<br> |
||
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
|- style="vertical-align:middle; background-color:#F8F9FA; color:#202122;" |
||
| − | | style="text-align:center;" | 14. ||Теорема об изменении кинетической энергии механической системы.||Механическая система приводится в движение из состояния покоя силой F = 20S, Н, приложенной к центру масс тела 1, где S - путь, пройденный центром масс тела 1. Масса барабана 2 равномерно распределена по его наружному ободу. В начальный момент времени пружина жесткости |
+ | | style="text-align:center;" | 14. ||Теорема об изменении кинетической энергии механической системы.||Механическая система приводится в движение из состояния покоя силой <math>F = 20S</math>, Н, приложенной к центру масс тела 1, где <math>S</math> - путь, пройденный центром масс тела 1. Масса барабана 2 равномерно распределена по его наружному ободу. В начальный момент времени пружина жесткости <math>C = 10</math> Н/м недеформирована <math>m_1 = m_2 = 10</math> кг, <math>R/r = 2</math>.<br> |
| − | Определить скорость центра масс тела 1, когда оно пройдет путь |
+ | Определить скорость центра масс тела 1, когда оно пройдет путь <math>S_1 = 2</math> м.<br> |
[[File:w23.png]]<br> |
[[File:w23.png]]<br> |
||
Latest revision as of 20:43, 17 April 2024
Теоретическая механика
- Квалификация выпускника: бакалавр
- Направление подготовки: 09.03.01 - “Информатика и вычислительная техника”
- Направленность (профиль) образовательной программы: Математические основы ИИ
- Программу разработал(а): Малолетов А.В.
1. Краткая характеристика дисциплины
Изучение дисциплины обеспечивает формирование и развитие компетенций обучающихся в области теоретической механики, их применение для решения различных прикладных задач в рамках профессиональной деятельности. В ходе освоения дисциплины обучающиеся рассматривают кинематику основных видов движения точек, твёрдых тел и их систем, равновесия механических систем, методы описания динамики движения механических систем, методы составления и решения математических моделей движения механических систем.
2. Перечень планируемых результатов обучения
- Целью освоения дисциплины является получение обучающимися фундаментальных знаний в области механического движения, равновесия материальных тел и возникающих между ними взаимодействиях, а также овладение основными алгоритмами исследования равновесия и движения механических систем.
- Задачами дисциплины являются
- усвоить основные законы механического движения и равновесия материальных тел;
- научиться анализировать и объяснять механические явления исходя из законов и теорем теоретической механики;
- уметь применять основные законы и методы теоретической механики к решению технических задач;
- приобрести навыки решения типовых задач по статике, кинематике и динамике;
- научиться методам построения математических моделей, оценивать их значение и относительность пределов применения.
Общая характеристика результата обучения по дисциплине
- Знания:
- сформированы систематические знания о методах описания кинематики точек, твёрдых тел и механизмов;
- сформированы систематические знания о равновесии твёрдых тел и механических систем;
- сформированы систематические знания о методах моделирования динамики материальных точек, твёрдых тел и механических систем.
- Умения:
- сформированы умения применять методы кинематики для описания законов движения точек, твёрдых тел и механизмов;
- сформированы умения применять методы статики для исследования равновесия твёрдых тел и механических систем;
- сформированы умения применять методы моделирования динамики материальных точек, твёрдых тел и механических систем;
- Навыки (владения):
- сформировано владение навыками расчёта законов движения и параметров механического состояния точек, твёрдых тел и механизмов;
- формировано владение навыками расчёта условий равновесия твёрдых тел и механических систем;
- сформировано владение навыками моделирования и расчёта динамики материальных точек, твёрдых тел и механических систем.
3. Структура и содержание дисциплины
| № п/п |
Наименование раздела дисциплины |
Содержание дисциплины по темам |
| 1. | Предмет кинематики. Кинематика точки и простейших движений твёрдых тел. | Пространство и время в классической механике. Система отсчета. Задачи кинематики. Векторный, координатный и естественный способы задания движения точки. Определение скорости и ускорения точки. Касательное и нормальное ускорение точки. Виды движений твердых тел. Поступательное движение твердого тела. Вращательное движение твердого тела вокруг неподвижной оси. Уравнение вращательного движения тела. Угловая скорость и угловое ускорение тела. Скорость и ускорение точки твердого тела вращающегося вокруг неподвижной оси. |
| 2. | Плоскопараллельное движение твердого тела. | Определение скорости точки плоской фигуры. Теорема о проекциях скоростей двух точек фигуры. Мгновенный центр скоростей, определение с его помощью скоростей точек плоской фигуры. Аналитический способ определения скорости точки плоской фигуры. Определение ускорений точек плоской фигуры. Кинематический расчет плоского механизма. |
| 3. | Сферическое движение. Общий случай движения твёрдого тела. | Теорема о конечном повороте твёрдого тела. Мгновенная ось вращения. Векторы угловой скорости и углового ускорения тела. Матрица поворота. Углы Эйлера. Самолётные и корабельные углы. Параметры Эйлера. Использование кватернионов для описания поворота твёрдого тела. Уравнения движения твердого тела вокруг неподвижной точки. Определение скоростей и ускорений точек тела. Уравнения движения свободного твердого тела. |
| 4. | Сложное движение. | Понятие о сложном (составном) движении. Составляющие сложного движения точки: относительное и переносное движение. Теорема о сложении скоростей. Кинематическая теорема Кориолиса. Определение Кориолисова ускорения. Сложное движение твёрдого тела. Определение угловых скоростей тела при сложном движении. |
| 5. | Сложное движение. | Понятие о сложном (составном) движении. Составляющие сложного движения точки: относительное и переносное движение. Теорема о сложении скоростей. Кинематическая теорема Кориолиса. Определение Кориолисова ускорения. Сложное движение твёрдого тела. Определение угловых скоростей тела при сложном движении. |
| 6. | Сложное движение. | Понятие о сложном (составном) движении. Составляющие сложного движения точки: относительное и переносное движение. Теорема о сложении скоростей. Кинематическая теорема Кориолиса. Определение Кориолисова ускорения. Сложное движение твёрдого тела. Определение угловых скоростей тела при сложном движении. |
| 7. | Предмет динамики. Динамика материальной точки. | Основные понятия и определения. Аксиомы динамики. Основное уравнение динамики материальной точки в инерциальной системе отсчёта. Две основные задачи динамики для материальной точки. Виды сил. Дифференциальные уравнения движения материальной точки в декартовых координатах и в проекциях на оси естественного трехгранника. Основное уравнение динамики материальной точки в неинерциальной системе отсчёта. Силы инерции. Принцип относительности в классической механике. Случай относительного покоя. |
| 8. | Механическая система. | Центр масс системы и его координаты. Классификация сил действующих на механическую систему. Свойства внутренних сил. Момент инерции системы и твердого тела относительно плоскости, оси и полюса. Радиус инерции. Теорема о моментах инерции относительно параллельных осей. Основные моменты инерции некоторых тел. |
| 9. | Теоремы о движении центра масс и количества движения. | Общие теоремы динамики и их значение. Теорема о движении центра масс системы. Количество движения точки и системы. Элементарный импульс и импульс силы за конечный промежуток времени. Теорема об изменении количества движения точки в дифференциальной и конечной формах. Теорема об изменении количества движения системы в дифференциальной и конечной формах. Случай сохранения количества движения. |
| 10. | Теорема об изменении кинетического момента. | Момент количества движения точки относительно центра и оси. Теорема об изменении момента количества движения точки. Главный момент количества движения или кинетический момент механической системы относительно центра и оси. Кинетический момент вращающегося твердого тела относительно оси вращения. Теорема об изменении кинетического момента системы. Теорема об изменении кинетического момента механической системы относительно ее центра масс. Случай сохранения кинетического момента. Элементарная теория гироскопа. |
| 11. | Дифференциальные уравнения движения твёрдого тела и системы твёрдых тел. | Дифференциальные уравнения поступательного, вращательного, плоско-параллельного, сферического и пространственного движений твердого тела. Дифференциальные уравнения движения системы твёрдых тел. |
| 12. | Метод кинетостатики. | Принцип Д’Аламбера для материальной точки. Сила инерции Д’Аламебера. Принцип Д’Аламбера для механической системы. Главный вектор и главный момент сил инерции. Приведение сил инерции твердого тела к центру. |
| 13. | Теорема об изменении кинетической энергии материальной точки. | Кинетическая энергия материальной точки и механической системы. Элементарная работа силы; ее аналитическое выражение. Работа силы на конечном пути. Работа силы тяжести силы, упругости и силы тяготения. Мощность. Теорема об изменении кинетической энергии точки в дифференциальной и конечной формах. Случай сохранения кинетической энергии. |
| 14. | Теорема об изменении кинетической энергии механической системы. | Вычисление кинетической энергии твердого тела в различных случаях его движения. Теорема об изменении кинетической энергии системы в дифференциальной и конечной формах. Понятие о силовом поле. Потенциальное силовое поле и силовая функция. Поверхности равного потенциала. Работа силы на конечном перемещении точки в потенциальном силовом поле. Потенциальная энергия. Случай сохранения механической энергии системы при действии на нее потенциальных сил. |
4. Методические и оценочные материалы
Задания для практических занятий:
Текущий контроль успеваемости обучающихся по дисциплине:
| № п/п |
Наименование раздела дисциплины |
Форма текущего контроля |
Материалы текущего контроля |
| 1. | Предмет кинематики. Кинематика точки и простейших движений твёрдых тел. | Устный / письменный опрос; | 1. Введение в кинематику
Предмет кинематики.
2. Кинематика точки
Способы задания движения точки.
3. Поступательное движение твердого тела.
Теорема о траекториях, скоростях и ускорениях точек тела при поступательном движении.
|
| 2. | Плоскопараллельное движение твердого тела. | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Плоскопараллельное или плоское движение твердого тела
Движение плоской фигуры и ее плоскости.
2. Определение скорости точки при плоскопараллельном движении.
Определение скорости точки плоской фигуры как геометрической суммы скорости полюса и скорости этой точки при вращении фигуры вокруг полюса (теорема о скоростях точек твердого тела при плоском движении).
3. Определение ускорения точки при плоскопараллельном движении.
Определение ускорения точки плоской фигуры как геометрической суммы ускорения полюса и ускорения этой точки во вращательном движении вместе с фигурой вокруг полюса (теорема об ускорениях точек твердого тела при плоском движении).
|
| 3. | Сферическое движение. Общий случай движения твёрдого тела. | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Сферическое движение или движение твёрдого тела с одной неподвижной точкой.
Теорема Эйлера о конечном повороте.
2. Общий случай движения твёрдого тела.
Разложение движения плоской фигуры на поступательное вместе с полюсом и сферическое вокруг полюса.
|
| 4. | Сложное движение | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Сложное движение точки.
Основные понятия сложного движения: относительное, переносное и абсолютное движение.
|
| 5. | Предмет статики. Плоская система сил. | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Предмет статики.
Основные понятия и определения: абсолютно твердое тело, материальная точка, сила. система сил и ее главный вектор, эквивалентные и уравновешенные системы сил, равнодействующая и уравнивающая силы.
2. Плоская система сил
Алгебраический и векторный момент силы относительно точки. Момент силы относительно оси.
|
| 6 | Произвольная система сил. Трение. | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Произвольная система сил
Приведение силы к заданному центру. Основная теорема статики о приведении произвольной системы сил.
2. Трение
Трение скольжения. Коэффициент трения скольжения. Угол и конус трения. Равновесие тела при наличии сил трения.
|
| 7 | Предмет динамики. Динамика материальной точки | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Предмет динамики.
Основные понятия и определения: масса, материальная точка, сила; постоянные и переменные силы.
2. Динамика материальной точки
Дифференциальные уравнения движения свободной материальной точки в векторной, координатной и естественной формах.
|
| 8 | Механическая система | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Механическая система.
Масса системы.
|
| 9 | Теоремы о движении центра масс и количества движения | Проверка выполнения домашних заданий; Устный / письменный опрос; | Общие теоремы динамики точки и системы.
Теорема о движении центра масс механической системы.
|
| 10 | Теорема об изменении кинетического момента | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Теорема об изменении кинетического момента
Кинетический момент (момент количества движения) точки и системы относительно центра и оси.
|
| 11 | Дифференциальные уравнения движения твёрдого тела и системы твёрдых тел | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Дифференциальные уравнения движения твёрдого тела
Дифференциальные уравнения поступательного движения твердого тела.
2. Дифференциальные уравнения движения системы твёрдых тел в форме Ньютона-Эйлера
Реакции связей между телами
|
| 12 | Метод кинетостатики | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Метод кинетостатики
Принцип Д’Аламбера для материальной точки.
|
| 13 | Теорема об изменении кинетической энергии материальной точки | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Теорема об изменении кинетической энергии материальной точки
Кинетическая энергия материальной точки
|
| 14 | Теорема об изменении кинетической энергии механической системы | Проверка выполнения домашних заданий; Устный / письменный опрос; | 1. Теорема об изменении кинетической энергии механической системы
Кинетическая энергия механической системы.
|
Контрольные вопросы для подготовки к промежуточной аттестации:
| № п/п |
Наименование раздела дисциплины |
Вопросы |
| 1. | Предмет кинематики. Кинематика точки и простейших движений твёрдых тел. | 1. Сформулируйте основные задачи кинематики. 2. Какие существую способы задания движения точки? |
| 2. | Плоскопараллельное движение твердого тела. | 1.Дайте определение плоскопараллельного движения твердого тела 2. Уравнения движения плоской фигуры. |
| 3. | Сферическое движение. Общий случай движения твёрдого тела. | 1. Дайте определение сферического движения или движения твёрдого тела с одной неподвижной точкой. 2. Теорема Эйлера о конечном повороте. |
| 4. | Сложное движение | 1. Основные понятия сложного движения: относительное, переносное и абсолютное движение. Скорости и ускорения в этих движениях. 2. Теорема о сложении скоростей в сложном движении точки. |
| 5. | Предмет статики. Плоская система сил. | 1. Дайте определения: абсолютно твердое тело, материальная точка, сила, система сил и ее главный вектор, эквивалентные и уравновешенные системы сил, равнодействующая и уравнивающая силы. 2. Сформулируйте основные задачи статики. |
| 6 | Произвольная система сил. Трение. | 1. Приведение силы к заданному центру. Основная теорема статики о приведении произвольной системы сил. 2. Главный вектор и главный момент произвольной системы сил. |
| 7 | Предмет динамики. Динамика материальной точки | 1. Дайте определения понятиям: масса, материальная точка, сила; постоянные и переменные силы. 2. Аксиомы динамики. |
| 8 | Механическая система | 1. Дайте определение понятиям: механическая система;
2. Сформулируйте свойства главных осей инерции. |
| 9 | Теоремы о движении центра масс и количества движения | 1. Теорема о движении центра масс механической системы. 2. Следствия из теоремы. |
| 10 | Теорема об изменении кинетического момента | 1. Кинетический момент (момент количества движения) точки и системы относительно центра и оси. 2. Момент количества движения вращающегося твердого тела относительно оси вращения. |
| 11 | Дифференциальные уравнения движения твёрдого тела и системы твёрдых тел | 1. Дифференциальные уравнения поступательного движения твердого тела. 2. Дифференциальное уравнение вращательного движения твердого тела. |
| 12 | Метод кинетостатики | 1. Принцип Д’Аламбера для материальной точки. 2. Сила инерции Д’Аламебера. |
| 13 | Теорема об изменении кинетической энергии материальной точки | 1. Кинетическая энергия материальной точки 2. Элементарная работа силы и ее аналитическое выражение. |
| 14 | Теорема об изменении кинетической энергии механической системы | 1. Кинетическая энергия механической системы. 2. Теорема Кенига. |
Вопросы/Задания к промежуточной аттестации в устной/письменной форме:
- Предмет статики. Основные понятия и определения: абсолютно твердое тело, материальная точка, сила. система сил и ее главный вектор, эквивалентные и уравновешенные системы сил, равнодействующая и уравнивающая силы. Основные задачи статики.
- Аксиомы статики. Сила - скользящий вектор. Принцип освобождаемости от связей. Деление сил на внешние и внутренние, активные и реакции связей.
- Связи и реакции связей. Реакции связей, осуществляемых в виде главных опор, нитей, цилиндрического и сферического шарниров. Реакции ненагруженного внешними силами стержня с шарнирами на концах. Реакции подвижных и неподвижных шарнирных опор. Жесткая заделка балки и ее реакции. Реакции шарнирного сочленения тел.
- Алгебраический и векторный момент силы относительно точки. Момент силы относительно оси. Связь между моментом силы относительно оси с векторным моментом силы относительно точки на оси. Аналитические выражения моментов сил относительно осей координат.
- Пара сил. Алгебраический и векторный моменты пары сил. Теорема о сумме моментов сил пары относительно произвольного центра.
- Теорема об эквивалентности двух пар сил, расположенных в одной плоскости.
- Теорема о переносе пары сил в параллельную плоскость. Момент пары сил- свободный вектор. Эквивалентность пар сил. Сложение пар сил. Условия равновесия произвольной системы пар сил.
- Приведение силы к заданному центру. Лемма о параллельном переносе силы. Основная теорема статики о приведении произвольной системы сил. Частный случай приведения плоской системы сил.
- Главный вектор и главный момент произвольной системы сил. Формулы для вычисления главного вектора и главного момента.
- Условия равновесия пространственной системы сил в векторной и аналитической формах. Частные случаи.
- Плоская система сил. Различные формы уравнений равновесия плоской системы сил.
- Частные случаи приведения плоской системы сил к простейшему виду. Случаи приведения к равнодействующей и к паре сил.
- Теорема о моменте равнодействующей произвольной системы сил относительно точки и оси (теорема Вариньона). Теорема Вариньона для плоской системы сил.
- Статически определимые и статически неопределимые задачи. Равновесие системы тел. Распределенные силы.
- Трение скольжения. Законы Кулона. Коэффициент трения скольжения. Угол и конус трения. Равновесие тела при наличии сил трения. (Равновесие тела на шероховатой поверхности).
- Трение качения. Коэффициент трения качения. Приближенные законы для наибольшего момента пары, препятствующей качению (законы трения качения).
- Соотношение между главными моментами системы сил относительно двух различных центров приведения. Инварианты системы сил.
- Частные случаи приведения пространственных систем сил к простейшим системам. Случай приведения пространственных систем сил к равнодействующей, к паре и к динамике. Уравнение центральной оси системы.
- Частные случаи равновесия твердого тела. Условия равновесия твердого тела с одной и двумя закрепленными точками.
- Пространственная система параллельных сил. Приведение к простейшим системам и условия равновесия пространственной системы параллельных сил.
- Центр системы параллельных сил. Радиус-вектор и координаты центра системы параллельных сил. Статические моменты системы параллельных сил.
- Центр тяжести твердого тела: центр тяжести объема, площади и линии. Методы нахождения центров тяжести тел и фигур сложной формы: центр тяжести симметричных однородных тел, метод разбиения тела на части, метод отрицательных масс (площадей), экспериментальные методы.
- Введение в кинематику. Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Система отсчета. Задачи кинематики.
- Кинематика точки. Векторный способ задания движения, уравнение движения. Годограф переменного вектора. Траектория, скорость и ускорение точки при векторном способе задания движения.
- Координатный способ задания движения точки. Уравнения движения точки в декартовых координатах. Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси. Уравнение годографа вектора скорости.
- Естественный способ задания движения точки. Дуговая координата, уравнение движения. Геометрические понятия; угол смежности, кривизна, радиус кривизны, естественные оси координат, естественный трехгранник. Скорость точки при естественном способе задания движения.
- Дифференцирование единичного вектора ускорения точки при естественном способе задания движения, нормальная и касательная составляющие ускорения.
- Частные случаи движения точки: прямолинейное и криволинейное, равномерное и переменное. Равнопеременное движение.
- Скорость и ускорение точки в полярных координатах. Радиальная и трансверсальная составляющие скорости и ускорения.
- Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек тела при поступательном движении.
- Вращение твердого тела вокруг неподвижной оси. Уравнение вращательного движения. Угловая скорость и угловое ускорение. Векторное изображение угловой скорости и углового ускорения. Равномерное и равнопеременное вращение твердого тела вокруг неподвижной оси.
- Определение скоростей и ускорений точек твердого тела, вращающегося вокруг неподвижной оси.
- Векторные выражения для скоростей и ускорений точек вращающегося твердого тела. Векторная формула Эйлера.
- Плоскопараллельное или плоское движение твердого тела и движение плоской фигуры и ее плоскости. Уравнения движения плоской фигуры. Уравнения движения произвольной точки плоской фигуры. Определение скорости и ускорения точки плоской фигуры с помощью этих уравнений.
- Разложение движения плоской фигуры на поступательное вместе с полюсом и вращательное вокруг полюса. Угловая скорость и угловое ускорение плоской фигуры и их независимость от выбора полюса.
- Определение скорости любой точки плоской фигуры как геометрической суммы скорости полюса и скорости этой точки при вращении фигуры вокруг полюса (теорема о скоростях точек твердого тела при плоском движении).
- Теорема о проекциях скоростей двух точек твердого тела на прямую проходящую через эти точки. Приложение этой теоремы к изучению скоростей точек твердого тела при плоском движении.
- Мгновенный центр скоростей. Теорема о его существовании и единственности в данный момент. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей.
- Способы нахождения положения мгновенного центра скоростей.
- Определение ускорения точки плоской фигуры как геометрической суммы ускорения полюса и ускорения этой точки во вращательном движении вместе с фигурой вокруг полюса (теорема об ускорениях точек твердого тела при плоском движении).
- Мгновенный центр ускорений. Определение ускорений точек твердого тела при плоском движении с помощью мгновенного центра ускорений.
- Сложное движение точки. Основные понятия сложного движения: относительное, переносное и абсолютное движение. Скорости и ускорения в этих движениях.
- Теорема о сложении скоростей в сложном движении точки.
- Теорема о сложении ускорений в общем случае сложного движения точки (кинематическая теорема Кориолиса).
- Определение модуля и направления ускорения Кориолиса. Правило Жуковского. Частные случаи, в которых ускорение Кориолиса равно нулю.
- Предмет динамики. Основные понятия и определения: масса, материальная точка, сила; постоянные и переменные силы. Законы классической механики или законы Галилея-Ньютона (аксиомы динамики). Инерциальная система отсчета. Задачи динамики.
- Дифференциальные уравнения движения свободной материальной точки. Векторная, координатная и естественная формы уравнений движения. Частные случаи. Две основные задачи динамики материальной точки. Решение первой задачи динамики.
- Вторая задача динамики точки. Интегрирование дифференциальных уравнений движения материальной точки в простейших случаях: прямолинейное движение под действием сил, зависящих только от времени, только от скорости или только от координаты (можно показать на примерах). Постоянные интегрирования и способы их определения.
- Вторая задача динамики точки. Интегрирование дифференциальных уравнений движения материальной точки в частный случаях криволинейного движения (показать на примере движения тела, брошенного под углом к горизонту).
- Механическая система (изменяемая и неизменяемая). Масса системы. Центр масс и его координаты. Статические моменты массы системы относительно полюса и плоскости. Статические моменты массы относительно центра масс и плоскостей, проходящих через центр масс.
- Моменты инерции системы и твердого тела относительно полюса, оси и плоскости. Радиус инерции. Теорема о моментах инерции относительно параллельных осей.
- Моменты инерции простейших однородных тел: стержня, кругового диска, прямого кругового цилиндра, шара.
- Момент инерции тела относительно оси произвольного направления (без вывода). Центробежные моменты инерции.
- Главные оси и главные моменты инерции. Главные оси инерции симметричных тел. Главные центральные оси инерции. Свойства главных осей инерции.
- Классификация сил, действующих на механическую систему: силы внутренние и внешние, задаваемые силы. Главный вектор и главный момент внутренних сил. Дифференциальные уравнения движения механической системы.
- Общие теоремы динамики точки и системы. Количество движения точки и системы. Элементарный и полный импульс силы. Теорема об изменении количества движения точки в дифференциальной и конечной формах. Теорема импульсов.
- Количество движения системы и способы его вычисления. Теорема об изменении количества движения системы в дифференциальной и конечной формах. Законы сохранения количества движения системы.
- Теорема о движении центра масс механической системы. Следствия из теоремы. Дифференциальные уравнения поступательного движения твердого тела.
- Момент количества движения точки и системы относительно центра и оси. Момент количества движения вращающегося твердого тела относительно оси вращения. Теорема об изменении момента количества движения для точки.
- Теорема об изменении момента количества движения для механической системы. Законы сохранения моментов количества движения. Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.
- Момент количества движения системы в абсолютном движении. Теорема об изменении момента количества движения системы в относительном движении по отношению к центру масс. #Дифференциальные уравнения плоского движения твердого тела.
- Элементарная работа силы и ее аналитическое выражение. Работа силы на конечном пути. Работа равнодействующей. Мощность.
- Примеры вычисления работы силы. Работа силы тяжести, линейной силы упругости и силы тяготения.
- Работа и мощность сил, приложенных к твердому телу при поступательном, вращательном и плоском движении твердого тела. Работа внутренних сил твердого тела.
- Кинетическая энергия материальной точки и системы. Теорема Кенига. Кинетическая энергия твердого тела в поступательном, вращательном и плоском движениях.
- Теорема об изменении кинетической энергии материальной точки и системы в дифференциальной и конечной формах. Случай абсолютно твердого тела.
- Понятие о силовом поле. Потенциальное силовое поле и силовая функция. Основные свойства силовой функции. Работа силы на конечном перемещении точки в потенциальном силовом поле. Поверхности равного уровня (потенциала) и их свойства. Потенциальная энергия.
- Примеры вычисления силовых функций потенциальных силовых полей: однородное поле силы тяжести, поле тяготения по закону Ньютона и поле линейной силы упругости. Законы сохранения механической энергии для точки и системы.
Перечень учебно-методического обеспечения дисциплины
Список основной литературы:
- Никитин, Н. Н. Курс теоретической механики [Текст] : учебник / Н. Н. Никитин. - Санкт-Петербург : Лань, 2011. - 720, [1] с.
- Никитин, Н. Н. Курс теоретической механики [Электронный ресурс] : учебник / Н. Н. Никитин. — Электрон. дан. — Санкт-Петербург : Лань, 2011. — 720 с. — Режим доступа: https://e.lanbook.com/book/1807
- Мещерский, И. В. Задачи по теоретической механике [Электронный ресурс] : учеб. пособие — Электрон. дан. — Санкт-Петербург : Лань, 2012. — 448 с. — Режим доступа: https://e.lanbook.com/book/2786
- Сборник заданий для курсовых работ по теоретической механике [Текст] : учеб. пособие / под ред. А. А. Яблонского. - Москва : Интеграл-Пресс, 2007. - 382 с.
Список дополнительной литературы:
- Бутенин, Н. В. Курс теоретической механики [Текст] : учеб. пособие / Н. В. Бутенин, Я. Л. Лунц, Д. Р. Меркин. - Санкт-Петербург : Лань, 2009. - 729 с.
- Бутенин, Н. В. Курс теоретической механики [Электронный ресурс] : учеб. пособие / Н.В. Бутенин, Я.Л. Лунц, Д.Р. Меркин. — Электрон. дан. — Санкт-Петербург : Лань, 2009. — 736 с. — Режим доступа: https://e.lanbook.com/book/29
- Бать, М. И. Теоретическая механика в примерах и задачах. Том 1: Статика и кинематика [Электронный ресурс] : учеб. пособие / М.И. Бать, Г.Ю. Джанелидзе, А.С. Кельзон. — Электрон. дан. — Санкт-Петербург : Лань, 2013. — 672 с. — Режим доступа: https://e.lanbook.com/book/4551
- Бать, М. И. Теоретическая механика в примерах и задачах. Том 2: Динамика [Электронный ресурс] : учеб. пособие / М.И. Бать, Г.Ю. Джанелидзе, А.С. Кельзон. — Электрон. дан. — Санкт-Петербург : Лань, 2013. — 640 с. — Режим доступа: https://e.lanbook.com/book/4552
- Тарг, С. М. Краткий курс теоретической механики [Текст] : учебник / С. М. Тарг.. - Москва : Высшая школа, 2003. - 416 с.
- Яблонский, А. А. Курс теоретической механики. Статика. Кинематика. Динамика [Текст] : учеб. пособие / А. А. Яблонский, В. М. Никифорова. - Москва : Интеграл-Пресс, 2007. - 608 с.
Методические указания для обучающихся по освоению дисциплины
| Вид учебных занятий/деятельности |
Деятельность обучающегося |
| Лекция | Написание конспекта лекций: кратко, схематично, последовательно фиксировать основные положения лекции, выводы, формулировки, обобщения; помечать важные мысли, выделять ключевые слова, термины. Обозначить вопросы, термины или другой материал, который вызывает трудности, пометить и попытаться найти ответ в рекомендуемой литературе. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия. |
| Практическое (семинарское) занятие | При подготовке к семинарскому (практическому) занятию необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме. На основании обработанной информации постараться сформировать собственное мнение по выносимой на обсуждение тематике. Обосновать его аргументами, сформировать список источников, подкрепляющих его. Во время семинарского (практического) занятия активно участвовать в обсуждении вопросов, высказывать аргументированную точку зрения на проблемные вопросы. Приводить примеры из источниковой базы и научной и/или исследовательской литературы. |
| Устный/письменный опрос | Отвечать, максимально полно, логично и структурировано, на поставленный вопрос. Основная цель – показать всю глубину знаний по конкретной теме или ее части. |
| Реферат | Поиск источников и литературы, составление библиографии. При написании реферата рекомендуется использовать разнообразные источники, монографии и статьи из научных журналов, позволяющие глубже разобраться в различных точках зрения на заданную тему. Изучение литературы следует начинать с наиболее общих трудов, затем следует переходить к освоению специализированных исследований по выбранной теме. Могут быть использованы ресурсы сети «Интернет» с соответствующими ссылками на использованные сайты. Если тема содержит проблемный вопрос, следует сформулировать разные точки зрения на него. Рекомендуется в выводах указать свое собственное аргументированное мнение по данной проблеме. Подготовить презентацию для защиты реферата. |
| Эссе | Написание прозаического сочинения небольшого объема и свободной композиции, выражающего индивидуальные впечатления и соображения по конкретному поводу или вопросу и заведомо не претендующего на определяющую или исчерпывающую трактовку предмета. При работе над эссе следует четко и грамотно формулировать мысли, структурировать информацию, использовать основные понятия, выделять причинно-следственные связи. Как правило эссе имеет следующую структуру: вступление, тезис и аргументация его, заключение. В качестве аргументов могут выступать исторические факты, явления общественной жизни, события, жизненные ситуации и жизненный опыт, научные доказательства, ссылки на мнение ученых и др. |
| Подготовка к промежуточной аттестации | При подготовке к промежуточной аттестации необходимо проработать вопросы по темам, которые рекомендуются для самостоятельной подготовки. При возникновении затруднений с ответами следует ориентироваться на конспекты лекций, семинаров, рекомендуемую литературу, материалы электронных и информационных справочных ресурсов, статей. Если тема вызывает затруднение, четко сформулировать проблемный вопрос и задать его преподавателю. |
| Практические (лабораторные) занятия | Практические занятия предназначены прежде всего для разбора отдельных сложных положений, тренировки аналитических навыков, а также для развития коммуникационных навыков. Поэтому на практических занятиях необходимо участвовать в тех формах обсуждения материала, которые предлагает преподаватель: отвечать на вопросы преподавателя, дополнять ответы других студентов, приводить примеры, задавать вопросы другим выступающим, обсуждать вопросы и выполнять задания в группах. Работа на практических занятиях подразумевает домашнюю подготовку и активную умственную работу на самом занятии. Работа на практических занятиях в форме устного опроса заключается прежде всего в тренировке навыков применять теоретические положения к самому разнообразному материалу. В ходе практических занятий студенты работают в группах для обсуждения предлагаемых вопросов. |
| Самостоятельная работа | Самостоятельная работа состоит из следующих частей: 1) чтение учебной, справочной, научной литературы; 2) повторение материала лекций; 3) составление планов устных выступлений; 4) подготовка видеопрезентации. При чтении учебной литературы нужно разграничивать для себя материал на отдельные проблемы, концепции, идеи. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис. |
| Видеопрезентация | Подготовка видеопрезентаций по курсу. Видеопрезентации могут быть сделаны на любую тему, затронутую в ходе курса. Темы должны быть заранее согласованы с преподавателем. Видеопрезентации продолжительностью около 5 минут (300 секунд) должны быть подготовлены в группах, определяемых преподавателем. Несмотря на то, что это групповая работа, должен явно присутствовать вклад каждого члена группы. |
| Доклад | Публичное, развернутое сообщение по определенной теме или вопросу, основанное на документальных данных. При подготовке доклада рекомендуется использовать разнообразные источники, позволяющие глубже разобраться в теме. Учебную литературу можно найти в электронных библиотечных системах, на которые подписан АНО Университет Иннополис. |
| Дискуссия | Публичное обсуждение спорного вопроса, проблемы. Каждая сторона должна оппонировать мнение собеседника, аргументируя свою позицию. |
| Контрольная работа | При подготовке к контрольной работе необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. |
| Тестирование (устное/письменное) | При подготовке к тестированию необходимо проработать материалы лекций, семинаров, основной и дополнительной литературы по заданной теме. Основная цель тестирования – показать уровень сформированности знаний по конкретной теме или ее части. |
| Индивидуальная работа | При выполнение индивидуальной работы необходимо взять задание у преподавателя, ознакомиться с требованиями к выполнению работы, изучить поставленную проблему, найти решение проблемы. Если самостоятельно не удается разобраться в материале, необходимо сформулировать вопрос и задать преподавателю на консультации, во время семинарского (практического) занятия. Оформить результаты работы. |
| Разработка отдельных частей кода | Разработать часть кода, исходя из поставленной задачи и рекомендаций преподавателя. При выполнении работы рекомендуется обращаться к материалам лекций и семинарских (практических) занятий. Если возникают затруднения, необходимо проконсультироваться с преподавателем. |
| Выполнение домашних заданий и групповых проектов | Для выполнения домашних заданий и групповых проектов необходимо получить формулировку задания от преподавателя и убедиться в понимании задания. При выполнение домашних заданий и групповых проектов необходимо проработать материалы лекций, основной и дополнительной литературы по заданной теме. |
Методы и технологии обучения, способствующие формированию компетенции
| Методы и технологии обучения, способствующие формированию компетенции |
| Информационно – коммуникационная технология, Технология проблемного обучения, Педагогика сотрудничества, Традиционные технологии, Модульная технология. |