BSc: Mathematical Analysis I.f22

Mathematical Analysis I

• Course name: Mathematical Analysis I
• Code discipline: CSE201
• Subject area: Math

Short Description

This calculus course covers differentiation and integration of functions of one variable, with applications. The basic objective of Calculus is to relate small-scale (differential) quantities to large-scale (integrated) quantities. This is accomplished by means of the Fundamental Theorem of Calculus. Should be understanding of the integral as a cumulative sum, of the derivative as a rate of change, and of the inverse relationship between integration and differentiation.

Course Topics

Course Sections and Topics

Section	Topics within the section
Derivatives	Derivative as a Limit Leibniz Notation Rates of Change The Chain Rule Fractional Powers and Implicit Differentiation Related Rates and Parametric Curves Inverse Functions and Differentiation Differentiation of the Trigonometric, Exponential and Logarithmic Functions Increasing and Decreasing Functions The Second Derivative and Concavity Maximum-Minimum Problems Graphing
Integrals	Sums and Areas The Fundamental Theorem of Calculus Definite and Indefinite Integrals Integration by Substitution Changing Variables in the Definite Integral Integration by Parts Trigonometric Integrals Partial Fractions Parametric Curves Applications of the integrals
Limits	Limits of Sequences Newton's Method Limits of Functions L'Hopital's Rule Improper integrals

Intended Learning Outcomes (ILOs)

What is the main purpose of this course?

This calculus course will provide an opportunity for participants to:

• understand key principles involved in differentiation and integration of functions
• solve problems that connect small-scale (differential) quantities to large-scale (integrated) quantities
• become familiar with the fundamental theorems of Calculus
• get hands-on experience with the integral and derivative applications and of the inverse relationship between integration and differentiation.

ILOs defined at three levels

We specify the intended learning outcomes at three levels: conceptual knowledge, practical skills, and comprehensive skills.

Level 1: What concepts should a student know/remember/explain?

By the end of the course, the students should be able to ...

• remember the differentiation techniques
• remember the integration techniques
• remember how to work with sequences and series

Level 2: What basic practical skills should a student be able to perform?

By the end of the course, the students should be able to ...

• apply the derivatives to analyse the functions
• integrate
• understand the basics of approximation

Level 3: What complex comprehensive skills should a student be able to apply in real-life scenarios?

By the end of the course, the students should be able to ...

• Take derivatives of various type functions and of various orders
• Integrate
• Apply definite integral
• Expand functions into Taylor series
• Apply convergence tests

Grading

Course grading range

Grade	Range	Description of performance
A. Excellent	90-100	-
B. Good	75-89	-
C. Satisfactory	60-74	-
D. Fail	0-59	-

Course activities and grading breakdown

Activity Type	Percentage of the overall course grade
Midterm	20
Quizzes	28 (2 for each)
Final exam	50
In-class participation	7 (including 5 extras)

Recommendations for students on how to succeed in the course

• Participation is important. Attending lectures is the key to success in this course.
• Review lecture materials before classes to do well.
• Reading the recommended literature is obligatory, and will give you a deeper understanding of the material.

Resources, literature and reference materials

Open access resources

• Jerrold E. Marsden and Alan Weinstein, Calculus I, II, and II. Springer-Verlag, Second Edition 1985
• Zorich, V. A. Mathematical Analysis I, Translator: Cooke R. (2004)

Software and tools used within the course

• No.

Activities and Teaching Methods

Teaching and Learning Methods within each section

Teaching Techniques	Section 1	Section 2	Section 3
Problem-based learning (students learn by solving open-ended problems without a strictly-defined solution)	0	0	0
Project-based learning (students work on a project)	1	1	1
Modular learning (facilitated self-study)	0	0	0
Differentiated learning (provide tasks and activities at several levels of difficulty to fit students needs and level)	1	1	1
Contextual learning (activities and tasks are connected to the real world to make it easier for students to relate to them)	0	0	0
Business game (learn by playing a game that incorporates the principles of the material covered within the course)	0	0	0
Inquiry-based learning	0	0	0
Just-in-time teaching	0	0	0
Process oriented guided inquiry learning (POGIL)	0	0	0
Studio-based learning	0	0	0
Universal design for learning	0	0	0
Task-based learning	0	0	0

Activities within each section

Learning Activities	Section 1	Section 2	Section 3
Lectures	1	1	1
Interactive Lectures	1	1	1
Lab exercises	1	1	1
Experiments	0	0	0
Modeling	0	0	0
Cases studies	0	0	0
Development of individual parts of software product code	0	0	0
Individual Projects	0	0	0
Group projects	0	0	0
Flipped classroom	0	0	0
Quizzes (written or computer based)	0	0	0
Peer Review	0	0	0
Discussions	1	1	1
Presentations by students	0	0	0
Written reports	0	0	0
Simulations and role-plays	0	0	0
Essays	0	0	0
Oral Reports	0	0	0

Formative Assessment and Course Activities

Ongoing performance assessment

Section 1

1. A plane curve is given by $x(t)=-{\frac {t^{2}+4t+8}{t+2}}$, ${\textstyle y(t)={\frac {t^{2}+9t+22}{t+6}}}$. Find

   the asymptotes of this curve;

   the derivative ${\textstyle y'_{x}}$.

2. Apply Leibniz formula Find ${\textstyle y^{(n)}(x)}$ if ${\textstyle y(x)=\left(x^{2}-2\right)\cos 2x\sin 3x}$.

   Draw graphs of functions

   Find asymptotes

3. Find the derivatives of the following functions:
   • ${\textstyle f(x)=\log _{|\sin x|}{\sqrt[{6}]{x^{2}+6}}}$;
   • ${\textstyle y(x)}$ that is given implicitly by ${\textstyle x^{3}+5xy+y^{3}=0}$.

Section 2

1. Find the following integrals:
   • ${\textstyle \int {\frac {{\sqrt {4+x^{2}}}+2{\sqrt {4-x^{2}}}}{\sqrt {16-x^{4}}}}\,dx}$;
   • ${\textstyle \int 2^{2x}e^{x}\,dx}$;
   • ${\textstyle \int {\frac {dx}{3x^{2}-x^{4}}}}$.
2. Find the indefinite integral ${\textstyle \displaystyle \int x\ln \left(x+{\sqrt {x^{2}-1}}\right)\,dx}$.
3. Find the length of a curve given by ${\textstyle y=\ln \sin x}$, ${\textstyle {\frac {\pi }{4}}\leqslant x\leqslant {\frac {\pi }{2}}}$.

Section 3

1. Find limits of the following sequences or prove that they do not exist:
   • $a_{n}=n-{\sqrt {n^{2}-70n+1400}}$;
   • ${\textstyle d_{n}=\left({\frac {2n-4}{2n+1}}\right)^{n}}$;
   • ${\textstyle x_{n}={\frac {\left(2n^{2}+1\right)^{6}(n-1)^{2}}{\left(n^{7}+1000n^{6}-3\right)^{2}}}}$.

Final assessment

Section 1

1. Solve the following linear programming problems.

   maximize $x_{1}+3x_{2}$

   subject to $-x_{1}-x_{2}\leq -3$

   $-x_{1}+x_{2}\leq -1$

   $-x_{1}+2x_{2}\leq 2$

   $x1,x2\geq 0$

2. Give an example showing that the variable that becomes basic in one iteration of the simplex method can become nonbasic in the next iteration.
3. Solve the given linear program using the dual–primal two phase algorithm.

   maximize $6x_{1}+8x_{2}+5x_{3}+9x_{4}$

   subject to $x_{1}+x_{2}+x_{3}+x_{4}=1$

   $x_{1},x_{2},x_{3},x_{4}\geq 0$

Section 2

1. Perform two iterations of the steepest descent method to minimize the function given from the stated starting point $(-1.2,1)$

   $f(x_{1},x_{2})=100(x_{2}-x_{1}^{2})^{2}+(1-x_{1})^{2}$

2. Minimize $f=2x_{1}^{2}+x_{2}^{2}$ by using the steepest descent method with the starting point $(1,2)$ (two iterations only).
3. Minimize $f=x_{1}^{2}+3x_{2}^{2}+6x_{3}^{2}$ by Newton's method using the starting point as $(2,-1,1)$ .

Section 3

• It is proposed to build thermal stations at three different sites. The total budget available is 3 units (1 unit = $10 million) and the feasible levels of investment on any thermal station are 0, 1, 2, or 3 units. The electric power obtainable (return function) for different investments is given below. Find the investment policy for maximizing the total electric power generated.

Return function Ri(x)	i = 1	i = 2	i = 3
R0(x)	0	0	0
R1(x)	2	1	3
R2(x)	4	5	5
R3(x)	6	6	6

• A fertilizer company needs to supply 50 tons of fertilizer at the end of the first month, 70 tons at the end of the second month, and 90 tons at the end of the third month. The cost of producing x tons of fertilizer in any month is given by $$(4500x+20x^{2})$. It can produce more fertilizer in any month and supply it in the next month. However, there is an inventory carrying cost of $400 per ton per month. Find the optimal level of production in each of the three periods and the total cost involved by solving it as an initial value problem.
• Consider the following tree solution for a minimum cost network flow problem:

  

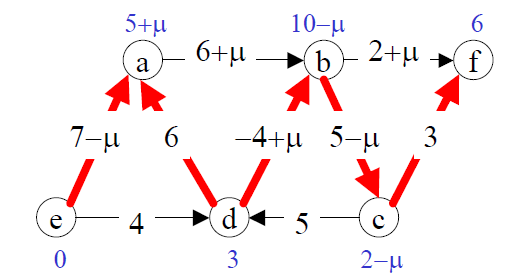
  As usual, bold arcs represent arcs on the spanning tree, numbers next to the bold arcs are primal flows, numbers next to non-bold arcs are dual slacks, and numbers next to nodes are dual variables.

  For what values of is this tree solution optimal?

  What are the entering and leaving arcs?

  After one pivot, what is the new tree solution?

  For what values of is the new tree solution optimal?

The retake exam

Retakes will be run as a comprehensive exam, where the student will be assessed the acquired knowledge coming from the textbooks, the lectures, the labs, and the additional required reading material, as supplied by the instructor. During such comprehensive oral/written the student could be asked to solve exercises and to explain theoretical and practical aspects of the course.