Difference between revisions of "BSc: IntroductionToCombinatoricsAndDiscreteMathematics"
V.matiukhin (talk | contribs) |
V.matiukhin (talk | contribs) |
||
| Line 117: | Line 117: | ||
|- style="background-color:#F8F9FA; color:#202122;" |
|- style="background-color:#F8F9FA; color:#202122;" |
||
| − | | style="text-align:center;" | || Основные правила комбинаторики || ''Принцип Дирихле. |
+ | | style="text-align:center;" |1 || Основные правила комбинаторики || ''Принцип Дирихле.'' Пусть есть <math>n</math> ящиков и <math>n+1</math> кроликов. Если расселить кроликов по ящикам, то найдется хотя бы один ящик, в котором окажутся не менее <math>2</math> кроликов. |
| Line 140: | Line 140: | ||
|- style="background-color:#F8F9FA; color:#202122;" |
|- style="background-color:#F8F9FA; color:#202122;" |
||
| − | | style="text-align:center;" | || Основные комбинаторные величины || Пусть <math>A = \{a_1, \dots, a_n\}</math>. Извлекать элементы из <math>A</math> можно по порядку или <<пригорошнями>>. Первые называются ''размещениями'', вторые --- ''сочетаниями''. При этом каждое из них бывает как с повторениями символов, так и без. |
+ | | style="text-align:center;" |2 || Основные комбинаторные величины || Пусть <math>A = \{a_1, \dots, a_n\}</math>. Извлекать элементы из <math>A</math> можно по порядку или <<пригорошнями>>. Первые называются ''размещениями'', вторые --- ''сочетаниями''. При этом каждое из них бывает как с повторениями символов, так и без. |
| − | + | * ''Размещением без повторений'' называется любой набор различных объектов <math>b_1,\dots,b_k \in A</math>, расположенных друг за другом в определенном порядке. Например, слова «лягушка» и «гуляшка» --- это два разных 7-размещения без повторений букв русского алфавита, хотя состоят они из одних и тех же букв. |
|
''Размещение с повторениями'' --- это снова любой набор объектов <math>b_1,\dots,b_k \in A</math>, расположенных друг за другом в определенном порядке. Только теперь объекты в размещении могут совпадать. Например, «жаба» и «абаж» --- два разных 4-размещения с повторениями из букв русского алфавита. |
''Размещение с повторениями'' --- это снова любой набор объектов <math>b_1,\dots,b_k \in A</math>, расположенных друг за другом в определенном порядке. Только теперь объекты в размещении могут совпадать. Например, «жаба» и «абаж» --- два разных 4-размещения с повторениями из букв русского алфавита. |
||
| Line 158: | Line 158: | ||
| − | (а) Сколько существует шестизначных чисел? |
+ | (а) Сколько существует шестизначных чисел? |
| + | |||
| + | (б) Сколько существует шестизначных чисел, делящихся на 5? |
||
| + | |||
| + | (в) Сколько существует шестизначных чисел, в записи которых присутствует хотя бы одна чётная цифра? |
||
| Line 171: | Line 175: | ||
Из класса, в котором учатся <math>28</math> человек, назначаются на дежурство в столовую <math>4</math> человека. |
Из класса, в котором учатся <math>28</math> человек, назначаются на дежурство в столовую <math>4</math> человека. |
||
| − | |||
| − | |||
| − | |||
Сколькими способами это можно сделать? |
Сколькими способами это можно сделать? |
||
| − | |||
| − | |||
Сколько существует способов набрать команду дежурных, в которую попадет ученик этого класса Коля Васин? |
Сколько существует способов набрать команду дежурных, в которую попадет ученик этого класса Коля Васин? |
||
| − | |||
| − | |||
В группе учатся <math>20</math> студентов. Согласно новому указу Минздрава <math>75%</math> группы нужно вакцинировать. |
В группе учатся <math>20</math> студентов. Согласно новому указу Минздрава <math>75%</math> группы нужно вакцинировать. |
||
| − | |||
| − | |||
| − | |||
Сколькими способами это можно сделать? |
Сколькими способами это можно сделать? |
||
| − | |||
| − | |||
Выяснилось, что один студент этой группы Коля Васин уже провакцинирован. Сколько теперь существует способов исполнить указ Минздрава? |
Выяснилось, что один студент этой группы Коля Васин уже провакцинирован. Сколько теперь существует способов исполнить указ Минздрава? |
||
| Line 237: | Line 229: | ||
|- style="background-color:#F8F9FA; color:#202122;" |
|- style="background-color:#F8F9FA; color:#202122;" |
||
| − | | style="text-align:center;" | || Тождества с биномиальными коэффициентами || |
+ | | style="text-align:center;" |3 || Тождества с биномиальными коэффициентами ||Покажите, что число <math>k</math>-сочетаний без повторений из <math>n</math>-элементного множества равно |
| − | |||
| − | Покажите, что число <math>k</math>-сочетаний без повторений из <math>n</math>-элементного множества равно |
||
| − | |||
| − | |||
а) Количеству последовательностей из 0 и 1 длины <math>n</math> с ровно <math>k</math> единицами. |
а) Количеству последовательностей из 0 и 1 длины <math>n</math> с ровно <math>k</math> единицами. |
||
| Line 251: | Line 239: | ||
г) (Бином Ньютона) Коэффициенту при мономе <math>a^kb^{n-k}</math> в разложении <math>(a+b)^n</math>. |
г) (Бином Ньютона) Коэффициенту при мономе <math>a^kb^{n-k}</math> в разложении <math>(a+b)^n</math>. |
||
| + | [[Image:pic1dm1.png]] |
||
| − | |||
| Line 262: | Line 250: | ||
- используя интерпретации выше |
- используя интерпретации выше |
||
| − | + | Докажите следующие тождества при целых неотрицательных<math>n,k</math>: |
|
а) <math>C_{n+1}^k = C_{n}^k+C_{n}^{k-1}</math> |
а) <math>C_{n+1}^k = C_{n}^k+C_{n}^{k-1}</math> |
||
| Line 272: | Line 260: | ||
| − | + | Найдите суммы при целых неотрицательных <math>n,k,m</math> : |
|
а) <math>C_{n}^0+ \ldots + C_{n}^n;</math> |
а) <math>C_{n}^0+ \ldots + C_{n}^n;</math> |
||
| Line 286: | Line 274: | ||
е) <math>C_{n}^0+\frac{1}{2} C_n^1 + \frac{1}{3} C_n^2 + \ldots + \frac{1}{n+1} C_{n}^n;</math> |
е) <math>C_{n}^0+\frac{1}{2} C_n^1 + \frac{1}{3} C_n^2 + \ldots + \frac{1}{n+1} C_{n}^n;</math> |
||
| − | ж) <math> |
+ | ж) <math>C_{n}^n + C_{n+1}^{n} + \ldots + C_{n+m}^{n};</math> |
з) <math>C_n^k+C_{n+1}^{k}+\ldots+C_{n+m}^{k};</math> |
з) <math>C_n^k+C_{n+1}^{k}+\ldots+C_{n+m}^{k};</math> |
||
| Line 299: | Line 287: | ||
н*) <math>C_{2n}^{0} - C_{2n-1}^{1} + C_{2n-2}^{2}+ \ldots + (-1)^nC_n^{n}.</math> |
н*) <math>C_{2n}^{0} - C_{2n-1}^{1} + C_{2n-2}^{2}+ \ldots + (-1)^nC_n^{n}.</math> |
||
| + | |||
| + | |||
Найдите <math>\sum_{(n_1,n_2,n_3), n_1+n_2+n_3=5, n_i \in \N } P(n_1,n_2,n_3) (-1)^{n_1+n_2}</math>. |
Найдите <math>\sum_{(n_1,n_2,n_3), n_1+n_2+n_3=5, n_i \in \N } P(n_1,n_2,n_3) (-1)^{n_1+n_2}</math>. |
||
| Line 307: | Line 297: | ||
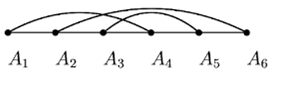
На оси абсцисс разместим (произвольным образом) 2n точек, разобьем множество этих точек на пары (опять-таки, произвольно) и элементы каждой пары соединим дугой, так, как это показано на рисунке. Получившийся объект назовем хордовой диаграммой. Сколько существует различных хордовых диаграмм на 2n точках? |
На оси абсцисс разместим (произвольным образом) 2n точек, разобьем множество этих точек на пары (опять-таки, произвольно) и элементы каждой пары соединим дугой, так, как это показано на рисунке. Получившийся объект назовем хордовой диаграммой. Сколько существует различных хордовых диаграмм на 2n точках? |
||
| + | [[Image:pic2dm1.png]] |
||
| − | * Найдите количество чисел, не превосходящих <math>1001</math> и не делящихся ни на одно из чисел <math>7</math>, <math>11</math>, <math>13</math>. |
||
| + | |||
| + | |||
| + | Найдите количество чисел, не превосходящих <math>1001</math> и не делящихся ни на одно из чисел <math>7</math>, <math>11</math>, <math>13</math>. |
||
| + | |||
| + | |||
| + | Пусть <math>\varphi(n)</math> --- ''функция Эйлера'', то есть количество натуральных чисел от <math>1</math> до <math>n</math>, взаимно простых c <math>n</math>. |
||
| + | |||
| + | |||
| + | Найдите <math>\varphi(1)</math>; <math>\varphi(p)</math>; <math>\varphi(p^2)</math>; <math>\varphi(p^{\alpha})</math>, где <math>p</math> --- простое число, <math>\alpha > 2</math>. |
||
| + | |||
| + | <math>\varphi(n) = n (1 - \frac{1}{p_1}) \ldots (1-\frac{1}{p_s})</math>, где <math>n=p_1^{\alpha_1}\cdot \ldots \cdot p_s^{\alpha_s}</math> --- каноническое разложение числа <math>n</math>. |
||
| − | * Пусть <math>\varphi(n)</math> --- ''функция Эйлера'', то есть количество натуральных чисел от <math>1</math> до <math>n</math>, взаимно простых c <math>n</math>. |
||
| − | ** Найдите <math>\varphi(1)</math>; <math>\varphi(p)</math>; <math>\varphi(p^2)</math>; <math>\varphi(p^{\alpha})</math>, где <math>p</math> --- простое число, <math>\alpha > 2</math>. |
||
| − | ** <math>\varphi(n) = n (1 - \frac{1}{p_1}) \ldots (1-\frac{1}{p_s})</math>, где <math>n=p_1^{\alpha_1}\cdot \ldots \cdot p_s^{\alpha_s}</math> --- каноническое разложение числа <math>n</math>. |
||
| + | В комнате площади <math>6</math> уложены три ковра площади <math>3</math> каждый (форма комнаты и ковров произвольная). Докажите, что какие-то два из этих трёх ковров перекрываются по площади, не меньшей~<math>1</math>. |
||
| + | На кафтане расположено пять заплат произвольной формы. Площадь каждой из них больше половины площади кафтана. Тогда площадь общей части некоторых двух заплат большей одной пятой площади кафтана. |
||
| − | * В комнате площади <math>6</math> уложены три ковра площади <math>3</math> каждый (форма комнаты и ковров произвольная). Докажите, что какие-то два из этих трёх ковров перекрываются по площади, не меньшей~<math>1</math>. |
||
| − | ** На кафтане расположено пять заплат произвольной формы. Площадь каждой из них больше половины площади кафтана. Тогда площадь общей части некоторых двух заплат большей одной пятой площади кафтана. |
||
(Число беспорядков) На полке стоят 10 книг. Сколькими способами их можно переставить так, чтобы (а) ни одна книга не осталась на своем месте? (б) на месте осталось ровно 4 книги? |
(Число беспорядков) На полке стоят 10 книг. Сколькими способами их можно переставить так, чтобы (а) ни одна книга не осталась на своем месте? (б) на месте осталось ровно 4 книги? |
||
| − | |||
Сколькими способами можно расселить 20 туристов по 5 домикам, чтобы ни один домик не оказался пустым? |
Сколькими способами можно расселить 20 туристов по 5 домикам, чтобы ни один домик не оказался пустым? |
||
| + | |||
Сколько существует различных сюръекций из множества X = {1, . . . , k} во множество Y = {1, . . . , n}? |
Сколько существует различных сюръекций из множества X = {1, . . . , k} во множество Y = {1, . . . , n}? |
||
| + | |||
Сколько существует неупорядоченных разбиений k-элементного множества на n подмножеств? |
Сколько существует неупорядоченных разбиений k-элементного множества на n подмножеств? |
||
| − | |||
В ряд записали 105 единиц, поставив перед каждой знак «+» . Сначала изменили знак на противоположный перед каждой третьей единицей, затем — перед каждой пятой, а затем — перед каждой седьмой. Найдите значение полученного выражения. 7 ◦ . Сколько существует перестановок чисел от 1 до 7, при которых никакие два рядом расположенных числа не отличаются на 1? |
В ряд записали 105 единиц, поставив перед каждой знак «+» . Сначала изменили знак на противоположный перед каждой третьей единицей, затем — перед каждой пятой, а затем — перед каждой седьмой. Найдите значение полученного выражения. 7 ◦ . Сколько существует перестановок чисел от 1 до 7, при которых никакие два рядом расположенных числа не отличаются на 1? |
||
| − | |||
[Задача о мажордомах] К обеду за круглым столом приглашены n пар враждующих рыцарей. Требуется рассадить их так, чтобы никакие два врага не сидели рядом. Сколько существует таких рассадок? |
[Задача о мажордомах] К обеду за круглым столом приглашены n пар враждующих рыцарей. Требуется рассадить их так, чтобы никакие два врага не сидели рядом. Сколько существует таких рассадок? |
||
| − | |||
| Line 344: | Line 340: | ||
|- style="background-color:#F8F9FA; color:#202122;" |
|- style="background-color:#F8F9FA; color:#202122;" |
||
| − | | style="text-align:center;" | || Рекуррентные соотношения || Для каждого из следующих линейных рекуррентных соотношений найдите общее решение: |
+ | | style="text-align:center;" |4 || Рекуррентные соотношения || Для каждого из следующих линейных рекуррентных соотношений найдите общее решение: |
а) <math>a_{n+2}- 7a_{n+1}+ 12a_n = 0;</math> |
а) <math>a_{n+2}- 7a_{n+1}+ 12a_n = 0;</math> |
||
| Line 350: | Line 346: | ||
б) <math>a_{n+3} - 2a_{n+2} - 4a_{n+1} + 8a_n = 0</math>; |
б) <math>a_{n+3} - 2a_{n+2} - 4a_{n+1} + 8a_n = 0</math>; |
||
| − | в) <math>a_{n+2} |
+ | в) <math>a_{n+2}+a_{n+1}+a_n=0;</math> |
г) <math>a_{n+2}- 9a_n = 0;</math> |
г) <math>a_{n+2}- 9a_n = 0;</math> |
||
| Line 356: | Line 352: | ||
д) <math>a_{n+3}+ 3a_{n+2}+ 3a_{n+1} + a_n= 0;</math> |
д) <math>a_{n+3}+ 3a_{n+2}+ 3a_{n+1} + a_n= 0;</math> |
||
| − | е) <math>a_{n+3} |
+ | е) <math>a_{n+3}+5a_{n+2}+12a_{n+1}+8a_n=0</math>. |
| − | |||
| − | |||
| Line 375: | Line 369: | ||
| − | |||
| − | === Задача === |
||
Найдите формулу для нахождения <math>n</math>-ого члена последовательности <math>F_n</math>. |
Найдите формулу для нахождения <math>n</math>-ого члена последовательности <math>F_n</math>. |
||
| − | |||
| − | === Задача === |
||
Найдите |
Найдите |
||
| Line 390: | Line 380: | ||
* <math>F_0^2+F_1^2+\ldots+F_n^2</math>; |
* <math>F_0^2+F_1^2+\ldots+F_n^2</math>; |
||
| − | * <math>F_0^3+ |
+ | * <math>F_0^3+F^_1^3+\idots+F_n^3</math>. |
| − | |||
| − | === Задача === |
||
Сколькими способами можно разменять купюру в <math>100</math> рублей на монеты достоинством <math>1</math>, <math>2</math> и <math>5</math> рублей? %364 |
Сколькими способами можно разменять купюру в <math>100</math> рублей на монеты достоинством <math>1</math>, <math>2</math> и <math>5</math> рублей? %364 |
||
| Line 400: | Line 388: | ||
| + | Найдите рекуррентное соотношение для последовательности <math>A_n</math>, где <math>A_n</math> -- число способов выложить прямоугольник размера |
||
| − | === Задача === |
||
| + | *<math>n \times 3</math>; |
||
| − | Найдите рекуррентное соотношение для последовательности <math>A_n</math>, где <math>A_n</math> --- |
||
| + | *<math>n \times 4</math> доминошками размера <math>1 \times 2</math>; |
||
| − | * число способов выложить прямоугольник размера |
||
| + | *число способов выложить колонну <math>2 \times 2\times n</math> кирпичами размера <math>2 \times 1 \times 1</math>. |
||
| − | ** <math>n \times 3</math>; |
||
| − | ** <math>n \times 4</math> доминошками размера <math>1 \times 2</math>; |
||
| − | ** число способов выложить колонну <math>2 \times 2\times n</math> кирпичами размера <math>2 \times 1 \times 1</math>. |
||
| − | |||
| − | |||
| − | |||
| − | === Задача === |
||
Сколько существует строк из <math>20</math> нулей и единиц, в каждой из которых никакие два нуля не стоят рядом? |
Сколько существует строк из <math>20</math> нулей и единиц, в каждой из которых никакие два нуля не стоят рядом? |
||
| Line 420: | Line 402: | ||
| + | Докажите, что последовательность с общим членом <math>a_n=n^{k-1}</math> удовлетворяет соотношению <math>a_{n+k} - C_{k}^1 a_{n+k-1} + C_k^2 a_{n+k-2} - \ldots + (-1)^k C_k^ka_n=0</math>. |
||
| − | === Задача === |
||
| − | |||
| − | Докажите, что последовательность с общим членом <math>a_n = n^{k-1}</math> удовлетворяет соотношению <math>a_{n+k} - C_{k}^1 a_{n+k-1} + C_k^2 a_{n+k-2} - \ldots + (-1)^k C_k^ka_n=0</math>. |
||
| − | |||
| Line 433: | Line 412: | ||
|- style="background-color:#F8F9FA; color:#202122;" |
|- style="background-color:#F8F9FA; color:#202122;" |
||
| − | | style="text-align:center;" | || Разбиения || |
+ | | style="text-align:center;" |5 || Разбиения || а) Найдите количество упорядоченных разбиений числа <math>n</math> на <math>k</math> слагаемых. |
б) Найдите общее количество упорядоченных разбиений числа <math>n</math> на слагаемые. |
б) Найдите общее количество упорядоченных разбиений числа <math>n</math> на слагаемые. |
||
| Line 445: | Line 424: | ||
| − | + | Справедливы следующие рекуррентные формулы |
|
а) <math>f(n;n_1,\ldots,n_k) = f(n-n_1;n_1,\ldots,n_k) + f(n-n_2;n_1,\ldots,n_k) + \ldots + f(n-n_k;n_1,\ldots,n_k)</math>; |
а) <math>f(n;n_1,\ldots,n_k) = f(n-n_1;n_1,\ldots,n_k) + f(n-n_2;n_1,\ldots,n_k) + \ldots + f(n-n_k;n_1,\ldots,n_k)</math>; |
||
| Line 455: | Line 434: | ||
| − | + | а) Что больше: <math>f(20;1,4,6,9)</math> или <math>F(20;1,4,6,9)</math>? б) Найдите оба числа, используя рекуррентные формулы. |
|
| − | Диаграмма Юнга |
+ | Диаграмма Юнга -- это конечный набор клеток, выровненных по левой границе, в котором длины строк образуют невозрастающую последовательность (каждая строка такой же длины как предыдущая, или короче). Весом диаграммы Юнга называется общее количество клеток диаграммы. Набор чисел, состоящий из длин строк, задаёт разбиение веса диаграммы в сумму слагаемых. Таким образом, есть соответствие между всеми неупорядоченными разбиениями натурального числа <math>n</math> и всеми диаграммами Юнга веса <math>n</math>. |
| − | + | Сколько существует диаграмм Юнга произвольного веса, но имеющих не более <math>p</math> строк и не более <math>q</math> столбцов? |
|
| − | + | На доске написано несколько целых положительных чисел: <math>a_0</math>, <math>a_1</math>, <math>a_2</math>, <math>\ldots</math>, <math>a_n</math>. Пишем на другой доске следующие числа: <math>b_0</math> --- сколько всего чисел на первой доске, <math>b_1</math> --- сколько там чисел, больших единицы, <math>b_2</math> --- сколько там чисел, больших двойки, и т.~д., пока получаются положительные числа. На этом заканчиваем --- нули не пишем. На третьей доске пишем числа <math>c_0</math>, <math>c_1</math>, <math>c_2</math>, <math>\ldots</math>, построенные по числам второй доски аналогичным образом. Докажите, что наборы чисел на первой и третьей досках совпадают. |
|
| − | доске следующие числа: <math>b_0</math> --- сколько всего чисел на первой доске, <math>b_1</math> --- сколько там чисел, больших единицы, <math>b_2</math> --- сколько там чисел, больших двойки, и т.~д., пока получаются положительные числа. На этом заканчиваем --- нули не пишем. На третьей доске пишем числа <math>c_0</math>, <math>c_1</math>, <math>c_2</math>, <math>\ldots</math>, построенные по числам второй доски |
||
| + | Докажите, что число неупорядоченных разбиений <math>a-b</math> на <math>c-1</math> слагаемых, не превосходящих <math>b</math>, равно числу неупорядоченных разбиений <math>a-c</math> на <math>b-1</math> слагаемых, не превосходящих <math>c</math>. |
||
| − | аналогичным образом. Докажите, что наборы чисел на первой и третьей досках совпадают. |
||
| + | Верно ли, что число неупорядоченных разбиений числа <math>n</math> на <math>k</math> слагаемых равно числу неупорядоченных разбиений числа <math>n</math> на слагаемые, максимальное из которых равно <math>k</math>? |
||
| − | \ii Докажите, что число неупорядоченных разбиений <math>a-b</math> на <math>c-1</math> слагаемых, не превосходящих <math>b</math>, равно числу неупорядоченных разбиений <math>a-c</math> на <math>b-1</math> слагаемых, не превосходящих <math>c</math>. |
||
| + | Докажите, что количество неупорядоченных разбиений <math>n</math> на различные нечётные слагаемые равно количеству симметричных диаграмм Юнга веса <math>n</math>. |
||
| + | Какие натуральные числа можно разбить в сумму нескольких (больше одного) подряд идущих натуральных чисел? |
||
| − | \ii Верно ли, что число неупорядоченных разбиений числа <math>n</math> на <math>k</math> слагаемых равно числу неупорядоченных разбиений числа <math>n</math> на слагаемые, максимальное из которых равно <math>k</math>? |
||
| + | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | | style="text-align:center;" | 6 || Формальные степенные ряды и производящие функции || Рассмотрим множество последовательностей <math>(a_0,a_1,\ldots,a_n,\ldots)</math> (здесь <math>a_i</math> берутся из множества чисел <math>\Q</math>, <math>\R</math> или <math>\C</math>) и введём на них операции сложения и умножения следующим образом: |
||
| − | \ii Докажите, что количество неупорядоченных разбиений <math>n</math> на различные нечётные слагаемые равно количеству симметричных диаграмм Юнга веса <math>n</math>. |
||
| + | <math>(a_0,a_1,\ldots) + (b_0,b_1,\ldots) = (a_0+b_0, a_1+b_1,\ldots);</math> |
||
| − | \istar Какие натуральные числа можно разбить в сумму нескольких (больше одного) подряд идущих натуральных чисел? |
||
| − | |- style="background-color:#F8F9FA; color:#202122;" |
||
| + | <math>(a_0,a_1,\ldots) \cdot (b_0,b_1,\ldots) = (c_0, c_1,\ldots) \text{, где } c_n = \sum_{j=0}^n a_j\cdot b_{n-j};</math> |
||
| − | | style="text-align:center;" | 6 || Формальные степенные ряды и производящие функции || Рассмотрим множество последовательностей <math>(a_0,a_1,\ldots,a_n,\ldots)</math> (здесь <math>a_i</math> берутся из множества чисел <math>\Q</math>, <math>\R</math> или <math>\C</math>) и введём на них операции сложения и умножения следующим образом: |
||
| − | <math>(a_0,a_1,\ldots) + (b_0,b_1,\ldots) = (a_0+b_0, a_1+b_1,\ldots);</math> |
||
| + | а) Пусть <math>1= (1,0,0,\ldots,0,\ldots)</math>, <math>t = (0,1,0,\ldots,0,\ldots)</math>. |
||
| − | <math>(a_0,a_1,\ldots) \cdot (b_0,b_1,\ldots) = (c_0, c_1,\ldots) \text{, где } c_n = \sum_{j=0}^n a_j\cdot b_{n-j};</math> |
||
| + | 1) Найдите <math>t^2, t^3, \idots, t^n</math>. |
||
| + | 2) Покажите, что любая последовательность <math>(a_0,a_1,\ldots,a_n,\ldots,)</math> единственным образом представляется в виде <math>a_0 \cdot 1 + a_1 \cdot t + a_2 \cdot t^2 + \ldots + a_n \cdot t^n + \ldots</math>. |
||
| − | \vspace*{-3mm} |
||
| + | 1) Покажите, что все свойства многочленов (коммутативность по сложению/умножению, ассоциативность, дистрибутивность) переносятся на формальные степенные ряды. |
||
| − | \begin{itemize} |
||
| + | 2) Пусть дан ряд <math>f(t)</math>. Корректна ли операция подстановки вместо <math>t</math> ряда <math>g(t)</math>? Ряда <math>g(t)</math> без свободного члена? |
||
| − | \item а) Пусть <math>1= (1,0,0,\ldots,0,\ldots)</math>, <math>t = (0,1,0,\ldots,0,\ldots)</math>. |
||
| − | \begin{itemize} |
||
| + | в) Определим ''производную'' формального степенного ряда <math>A = a_0 \cdot 1 + a_1 \cdot t + \ldots + a_n \cdot t^n + \ldots</math> как ряд <math>A' = a_1 + 2a_2 t + \ldots + n a_n t^{n-1} + \ldots</math>. Производную можно брать несколько раз подряд, через <math>A^{(n)}</math> обозначается <math>n</math>-ая производная ряда <math>A</math>. |
||
| − | \item 1) Найдите <math>t^2,t^3,\ldots,t^n</math>. |
||
| − | \item 2) Покажите, что любая последовательность <math>(a_0,a_1,\ldots,a_n,\ldots,)</math> единственным образом представляется в виде <math>a_0 \cdot 1 + a_1 \cdot t + a_2 \cdot t^2 + \ldots + a_n \cdot t^n + \ldots</math>. |
||
| − | \end{itemize} |
||
| + | 1) Производная линейна, то есть <math>(\alpha A + \beta B)' = \alpha A' + \beta B'</math> (здесь <math>\alpha,\beta \in \R</math>, <math>A,B</math> --- формальные степенные ряды). |
||
| − | \item б) Выражения <math>a_0 \cdot 1 + a_1 \cdot t + a_2 \cdot t^2 + \ldots + a_n \cdot t^n + \ldots</math> ( с введёнными операциями сложения и умножения) называют ''формальными степенными рядами''. <math>a_0</math> называют ''свободным членом'' ряда. |
||
| + | 2) Выполнено ''тождество Лейбница'', то есть <math>(AB)' = A'B + AB'</math>. |
||
| − | \begin{itemize} |
||
| + | 3) (''Ряд Тейлора в нуле''). Докажите, что <math>a_n</math> --- свободный член ряда <math>\frac{A^{(n)}}{n!}</math>. |
||
| − | \item 1) Покажите, что все свойства многочленов (коммутативность по сложению/умножению, ассоциативность, дистрибутивность) переносятся на формальные степенные ряды. |
||
| − | \item 2) Пусть дан ряд <math>f(t)</math>. Корректна ли операция подстановки вместо <math>t</math> ряда <math>g(t)</math>? Ряда <math>g(t)</math> без свободного члена? |
||
| + | Пусть <math>F=1+t+t^2+\dots</math>, <math>G=1-t+t^2-t^3+\dots</math>. Найдите <math>F+G</math>, <math>F\cdot G</math>. |
||
| − | \end{itemize} |
||
| − | \item в) Определим ''производную'' формального степенного ряда <math>A = a_0 \cdot 1 + a_1 \cdot t + \ldots + a_n \cdot t^n + \ldots</math> как ряд <math>A' = a_1 + 2a_2 t + \ldots + n a_n t^{n-1} + \ldots</math>. Производную можно брать несколько раз подряд, через <math>A^{(n)}</math> обозначается <math>n</math>-ая производная ряда <math>A</math>. |
||
| + | Пусть <math>F = \sum_{k=0}^{\infty} \frac{1}{k!}t^k</math>, <math>G = \sum_{k=0}^{\infty} \frac{(-1)^k}{k!}t^k</math>. Найдите <math>F \cdot G</math> и <math>F^2</math>. |
||
| − | \begin{itemize} |
||
| − | \item 1) Производная линейна, то есть <math>(\alpha A + \beta B)' = \alpha A' + \beta B'</math> (здесь <math>\alpha,\beta \in \R</math>, <math>A,B</math> --- формальные степенные ряды). |
||
| + | Существует ли два таких ненулевых степенных ряда <math>F,G</math>, что <math>F\cdot G = F+G</math>? |
||
| − | \item 2) Выполнено ''тождество Лейбница'', то есть <math>(AB)' = A'B + AB'</math>. |
||
| − | \item 3) (''Ряд Тейлора в нуле''). Докажите, что <math>a_n</math> --- свободный член ряда <math>\frac{A^{(n)}}{n!}</math>. |
||
| + | Ряд <math>G</math> называется ''обратимым'', если существует такой ряд <math>F</math>, что <math>F\cdot G=1</math>. <math>F</math> называется ''рядом, обратным к <math>G</math>'' и обозначается так: <math>F = G^{-1}</math>. |
||
| − | \end{itemize} |
||
| − | \end{itemize} |
||
| + | Докажите, что ряд <math>G = a_0+ a_1 t + a_2 t^2 + a_3 t^3+ \dots</math> обратим тогда и только тогда, когда <math>a_0 \neq 0</math>, причём обратный ряд <math>G^{-1}</math> единственен. |
||
| − | \begin{itemize} |
||
| + | Найдите коэффициенты ряда $\frac{1}{1-t}$; $\frac1{2-t}$; $\frac1{3+4t}$; $\frac1{(1-t)^{2}}$; $\frac1{(1-t)^{m}}$. |
||
| − | \item г) Пусть <math>F=1+t+t^2+\dots</math>, <math>G=1-t+t^2-t^3+\dots</math>. Найдите <math>F+G</math>, <math>F\cdot G</math>. |
||
| − | \begin{itemize} |
||
| − | \item 1) Пусть <math>F = \sum_{k=0}^{\infty} \frac{1}{k!}t^k</math>, <math>G = \sum_{k=0}^{\infty} \frac{(-1)^k}{k!}t^k</math>. Найдите <math>F \cdot G</math> и <math>F^2</math>. |
||
| + | Верно ли равенство $\left(\frac{1}{1-t}\right)^2 \cdot \left(\frac{1}{1+t}\right)^2 = \left(\frac{1}{1-t^2}\right)^2$ для формальных степенных рядов? |
||
| − | \end{itemize} |
||
| − | \item д) Существует ли два таких ненулевых степенных ряда <math>F,G</math>, что <math>F\cdot G = F+G</math>? |
||
| − | \begin{itemize} |
||
| + | Сформулируйте комбинаторное тождество, получаемое при приравнивании коэффициентов в этих рядах. |
||
| − | \item Ряд <math>G</math> называется ''обратимым'', если существует такой ряд <math>F</math>, что <math>F \cdot G = 1</math>. <math>F</math> называется ''рядом, обратным к <math>G</math>'' и обозначается так: <math>F = G^{-1}</math>. |
||
| − | \end{itemize} |
||
| − | \item е) Докажите, что ряд <math>G = a_0+ a_1 t + a_2 t^2 + a_3 t^3+ \dots</math> обратим тогда и только тогда, когда <math>a_0 \neq 0</math>, причём обратный ряд <math>G^{-1}</math> единственен. |
||
| + | При каких условиях на степенной ряд <math>F</math> его можно разделить на степенной ряд <math>G</math> (то есть уравнение <math>G\cdot X=F</math> разрешимо относительно неизвестного степенного ряда <math>X</math>)? |
||
| − | \item ё) Найдите коэффициенты ряда $\frac{1}{1-t}$; $\frac1{2-t}$; $\frac1{3+4t}$; $\frac1{(1-t)^{2}}$; $\frac1{(1-t)^{m}}$. |
||
| − | \item ж) Верно ли равенство $\left(\frac{1}{1-t}\right)^2 \cdot \left(\frac{1}{1+t}\right)^2 = \left(\frac{1}{1-t^2}\right)^2$ для формальных степенных рядов? |
||
| − | \begin{itemize} |
||
| + | При каких условиях на степенной ряд <math>F</math> разрешимо уравнение <math>X^2=F</math>? |
||
| − | \item Сформулируйте комбинаторное тождество, получаемое при приравнивании коэффициентов в этих рядах. |
||
| − | \end{itemize} |
||
| − | \item з) При каких условиях на степенной ряд <math>F</math> его можно разделить на степенной ряд <math>G</math> (то есть уравнение <math>G \cdot X = F</math> разрешимо относительно неизвестного степенного ряда <math>X</math>)? |
||
| + | Пусть <math>X = \sum_{k=0}^{\infty} \alpha_k t^k</math> ---- степенной ряд, задаваемый уравнением <math>X^2 = 1+t</math>. Найдите коэффициенты <math>\alpha_0,\alpha_1,\alpha_2,\alpha_3</math>. |
||
| − | \begin{itemize} |
||
| − | \item 1) При каких условиях на степенной ряд <math>F</math> разрешимо уравнение <math>X^2=F</math>? |
||
| − | \item 2) Пусть <math>X = \sum_{k=0}^{\infty} \alpha_k t^k</math> ---- степенной ряд, задаваемый уравнением <math>X^2=1+t</math>. Найдите коэффициенты <math>\alpha_0,\alpha_1,\alpha_2,\alpha_3</math>. |
||
| + | Пусть <math>\alpha \in \R</math>. Положим <math>C_{\alpha}^n = \frac{\alpha \cdot (\alpha-1) \cdot \ldots \cdot (\alpha-n+1)}{n!}</math>. |
||
| − | \end{itemize} |
||
| − | \item и) Пусть <math>\alpha \in \R</math>. Положим <math>C_{\alpha}^n = \frac{\alpha \cdot (\alpha-1) \cdot \ldots \cdot (\alpha-n+1)}{n!}</math>. |
||
| − | \begin{itemize} |
||
| − | + | Если <math>\alpha \in \N, \alpha \geq n</math>, то <math>C_{\alpha}^n</math> совпадает с биномиальным коэффициентом. |
|
| − | \item 2) <math>C_{\alpha + \beta }^n = \sum_{j=0}^n C_{\alpha}^j \cdot C_{\beta}^{n-j}</math>. |
||
| − | \item 3) Определим ряд <math>(1+t)^\alpha = \sum_{n=0}^{\infty} C_{\alpha}^n t^n</math>. Покажите, что при <math>\alpha\in \N</math> определения согласованы. |
||
| + | Определим ряд <math>(1+t)^\alpha = \sum_{n=0}^{\infty} C_{\alpha}^n t^n</math>. Покажите, что при <math>\alpha\in \N</math> определения согласованы. |
||
| − | \item 4) Покажите, что <math>(1+t)^{\alpha} \cdot (1+t)^{\beta} = (1+t)^{\alpha+\beta}</math>. |
||
| − | \item 5) Используя определение, найдите коэффициенты ряда <math>(1+t)^{\frac{1}{2}}</math>. Сравните ответ с ответом в задаче предыдущей задаче пункте в. |
||
| − | \end{itemize} |
||
| + | Покажите, что <math>(1+t)^{\alpha} \cdot (1+t)^{\beta} = (1+t)^{\alpha+\beta}</math>. |
||
| − | \end{itemize} |
||
| + | Используя определение, найдите коэффициенты ряда <math>(1+t)^{\frac{1}{2}}</math>. Сравните ответ с ответом в задаче предыдущей задаче пункте в. |
||
| − | * Вычислите <math>\sum_{k=0}^n k^2 C_n^k {(\frac{1}{17})}^k</math>. |
||
| − | * Вычислите <math>\sum_{k=0}^{\infty} \frac{F_n}{2^n}</math> (<math>F_n</math> --- числа Фибоначчи). |
||
| + | |||
| + | Вычислите <math>\sum_{k=0}^n k^2 C_n^k {(\frac{1}{17})}^k</math>. |
||
| + | |||
| + | |||
| + | Вычислите <math>\sum_{k=0}^{\infty} \frac{F_n}{2^n}</math> (<math>F_n</math> --- числа Фибоначчи). |
||
| − | === Задача === |
||
* Как выглядит производящая функция для числа способов набрать <math>n</math> рублей монетами достоинством <math>1</math>, <math>2</math> и <math>5</math> рублей? |
* Как выглядит производящая функция для числа способов набрать <math>n</math> рублей монетами достоинством <math>1</math>, <math>2</math> и <math>5</math> рублей? |
||
| Line 617: | Line 573: | ||
| − | |||
| − | === Задача === |
||
Найдите производящую функцию для числа |
Найдите производящую функцию для числа |
||
| Line 633: | Line 587: | ||
| − | |||
| − | === Задача === |
||
* Докажите тождество <math>4^n = \sum\limits_{i=0}^n C_{2i}^{i} \cdot C_{2(n-i)}^{n-i}</math>. |
* Докажите тождество <math>4^n = \sum\limits_{i=0}^n C_{2i}^{i} \cdot C_{2(n-i)}^{n-i}</math>. |
||
| − | * Вычислите сумму <math>(C_n^0)^2-(C_n^1)^2+\ldots+(-1)^n(C_n^n)^2</math>. |
||
| + | Найдите радиус сходимости ряда |
||
| − | '''Теорема Коши-Адамара.''' Пусть <math>\frac1R = {\overline{\lim\limits_{n \to \infty}} \sqrt[n]{|a_n|}}</math>. Тогда ряд <math>\sum\limits_{n=0}^{\infty} a_nt^n</math> сходится при <math>|t|<R</math> и расходится при <math>|t|>R</math>, таким образом функция <math>f(t) = \sum\limits_{n=0}^{\infty} a_nt^n</math> определена в каждой точке множества <math>\{t \mid |t| < R\}</math>. Число <math>R</math> называется ''радиусом сходимости ряда''. |
||
| + | <math>\sum_{n=0}^{\infty} t^n</math>, |
||
| + | <math>\sum_{n=0}^{\infty} (-1)^n \cdot t^n</math>, |
||
| − | + | <math>\sum_{n=0}^{\infty} \lambda^n t^n</math>, |
|
| + | <math>\frac{1}{1-t^2}</math>. |
||
| + | Приведите пример, когда на границе ряда (то есть при <math>|t|=R</math>) есть сходимость в обеих точках; <math>\sum_{n=0}^{\infty}</math> расходимость в обеих точках; <math>\sum_{n=0}^{\infty}</math> сходимость в одной точке и расходимость в другой точке. |
||
| − | |||
| − | Приведите пример, когда на границе ряда (то есть при <math>|t|=R</math>) есть <math>сходимость в обеих точках; \sum_{n=0}^{\infty} расходимость в обеих точках; \sum_{n=0}^{\infty} сходимость в одной точке и расходимость в другой точке</math>. |
||
| − | |||
| − | |||
Найдите производящую функцию для последовательности <math>a_n = C_1 \lambda_1^n + C_2 \lambda_2^n</math>. \pu Какой у неё радиус сходимости? |
Найдите производящую функцию для последовательности <math>a_n = C_1 \lambda_1^n + C_2 \lambda_2^n</math>. \pu Какой у неё радиус сходимости? |
||
| − | |||
| − | |||
Revision as of 14:42, 3 April 2024
Введение в комбинаторику и дискретную математику
- Квалификация выпускника: бакалавр
- Направление подготовки: 09.03.01 - “Информатика и вычислительная техника”
- Направленность (профиль) образовательной программы: Математические основы ИИ
- Программу разработал(а):
1. Краткая характеристика дисциплины
Изучение дисциплины обеспечивает формирование и развитие компетенций обучающихся в области комбинаторики и дискретной математики, их применение для решения различных прикладных задач в рамках профессиональной деятельности. В ходе освоения дисциплины обучающиеся рассматривают основные правила комбинаторики (сложение, умножение, принцип Дирихле, формула включений и исключений), концепции (числа сочетаний и размещений, рекуррентные соотношения, разбиения, формальные степенные ряды и производящие функции).
2. Перечень планируемых результатов обучения
- Целью освоения дисциплины
- Задачами дисциплины являются изучение основных правил и концепций комбинаторики для различных прикладных задач.
Общая характеристика результата обучения по дисциплине
- Знания: сформированы систематические знания по комбинаторике и дискретной математики.
- Умения:
- Навыки (владения):
3. Структура и содержание дисциплины
| № п/п |
Наименование раздела дисциплины |
Содержание дисциплины по темам |
| 1. | Основные правила комбинаторики | - правило сложения
- правило умножения - правило дополнения - принцип Дирихле |
| 2. | Основные комбинаторные величины | - размещения с повторениями / без повторений
- сочетания с повторениями/ без повторений - перестановки - треугольник Паскаля - линейный город - биномиальный и полиномиальный коэффициент |
| 3. | Тождества с биномиальными коэффициентами | - симметричность
- унимодальность - рекуррентное соотношение - Бином Ньютона - сумма биномиальных коэффициентов (в том числе альтернированная) - сумма квадратов биномиальных коэффициентов - сумма степеней натуральных чисел - формула включений и исключений - число беспорядков |
| 4. | Рекуррентные соотношения | - линейные однородные рекуррентные соотношения
- л.о.р.с. для степени 2 с разными корнями - л.о.р.с. для степени 2 с кратным корнем - формулировка теоремы в общем случае - числа Фибоначчи - формулировка теоремы для неоднородного случая |
| 5. | Разбиения | - упорядоченные и неупорядоченные разбиения
- диаграммы Юнга - теоремы Эйлера о равенстве неупорядоченных разбиений - асимптотика неупорядоченных разбиений |
| 6 | Формальные степенные ряды и производящие функции | - формальные степенные ряды
- обратимость ряда, пример деления в столбик - доказательство комб. тождеств при помощи формального степенного ряда - производящие функции для рекуррентных соотношений - возведение ряда в степень - числа Каталана |
4. Методические и оценочные материалы
Задания для практических занятий:
| № п/п |
Наименование раздела дисциплины (модуля) |
Перечень рассматриваемых тем (вопросов) |
| 1 | Основные правила комбинаторики | Принцип Дирихле. Пусть есть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
ящиков и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n+1}
кроликов. Если расселить кроликов по ящикам, то найдется хотя бы один ящик, в котором окажутся не менее Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2}
кроликов.
В мешке имеется Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 32} красных шара, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 29} зеленых шаров, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 45} синих, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 17} желтых и по Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 30} белых, черных и серых (всего Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 213} шаров). Сколько шаров необходимо вынуть из мешка, чтобы среди них гарантированно нашлось Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 9} шаров одного цвета?
Комиссия из Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 60} человек провела Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 40} заседаний, причем на каждом заседании присутствовали ровно Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10} членов комиссии. Докажите, что найдутся два члена комиссии, по крайней мере дважды встречавшиеся на заседаниях.
В таблице Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10 \times 10} расставлены целые числа, причем любые два числа в соседних клетках отличаются не более, чем на Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5} . Докажите, что среди этих чисел найдутся два равных.
Пусть имеется множество из Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} слов в алфавите из Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k>1} символа. Докажите, что хотя бы одно из слов не короче Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log_k{M}} .
В правильном треугольнике со стороной Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} отмечено пять точек. Докажите, что найдется пара точек, удаленных друг от друга не более, чем на Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2} . |
| 2 | Основные комбинаторные величины | Пусть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \{a_1, \dots, a_n\}}
. Извлекать элементы из Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
можно по порядку или <<пригорошнями>>. Первые называются размещениями, вторые --- сочетаниями. При этом каждое из них бывает как с повторениями символов, так и без.
Размещение с повторениями --- это снова любой набор объектов Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1,\dots,b_k \in A} , расположенных друг за другом в определенном порядке. Только теперь объекты в размещении могут совпадать. Например, «жаба» и «абаж» --- два разных 4-размещения с повторениями из букв русского алфавита. Сочетания без повторений отличаются от размещений без повторений тем, что в них порядок объектов значения не имеет. Так, «лягушка» и «гуляшка» представляют собой одно и то же 7-сочетание без повторений букв {л, я, г, у, ш, к, а } русского алфавита. Сочетания с повторениями аналогично, например { ж, а, б, а } = { а, б, а, ж }.
Сформулируйте на языке теории множеств что такое размещение с повторениями/ без повторений и сочетания с повторениями (не используя понятий набор и порядок, разрешается использовать все определения из первых двух листков, например: множество, элемент, подмножество, все виды отображений, декартово произведение). Докажите формулу для числа размещений без повторений (если вы будете пользоваться правилом умножения, сформулируйте чётко, какие множества A и B вы используете).
(а) Сколько существует шестизначных чисел? (б) Сколько существует шестизначных чисел, делящихся на 5? (в) Сколько существует шестизначных чисел, в записи которых присутствует хотя бы одна чётная цифра?
На плоскости отмечено 10 точек так, что никакие три из них не лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках?
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 20} балбесов-первокурсников и семинарист пришли в кинотеатр и сели в одном ряду. Семинарист должен сидеть с краю, а Петю, Колю и Васю нельзя сажать втроем. Сколькими способами можно рассадить группу?
Из класса, в котором учатся Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 28} человек, назначаются на дежурство в столовую человека. Сколькими способами это можно сделать? Сколько существует способов набрать команду дежурных, в которую попадет ученик этого класса Коля Васин? В группе учатся Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 20} студентов. Согласно новому указу Минздрава Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 75%} группы нужно вакцинировать. Сколькими способами это можно сделать? Выяснилось, что один студент этой группы Коля Васин уже провакцинирован. Сколько теперь существует способов исполнить указ Минздрава?
У королевы есть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 12} одинаковых зеркал. Сколькими способами их можно повесить в Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 8} разных залах замка так, чтобы в каждом зале было хотя бы одно зеркало?
В пекарне продавались Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4} вида пирожков: элеши, эчпочмаки, перемячи и кыстыбыи. Сколькими способами можно купить Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 7} пирожков?
Есть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} попарно различных чашек и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} неразличимых стаканов. Также имеется Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} попарно различных ложек и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} неразличимых кусков сахара. Сколькими способами можно разложить: а) ложки по чашкам; б) сахар по чашкам; в) ложки по стаканам, если Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 4} ?
На ютуб-канале есть плейлист из Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 30} лекций по ДМ. Сколькими способами их можно переставить так, чтобы а) шесть лекций, прочитанных Даниилом Владимировичем, расположились в правильном порядке (но не обязательно подряд)? б) те же лекции по-прежнему были в правильном порядке, но никакие в) две из них не шли подряд?
Сколько имеется способов раздать Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 11} разных цветков, трём девушкам: какой-то --- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5} , а остальным~--- по Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3} цветка?
Дано множество Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \{1, \dots , n\}} . Даны числа Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} .
Сколькими способами можно выбрать из полной колоды, содержащей Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 52} карты, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6} карт так, чтобы среди них были все Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4} масти? |
| 3 | Тождества с биномиальными коэффициентами | Покажите, что число Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
-сочетаний без повторений из Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
-элементного множества равно
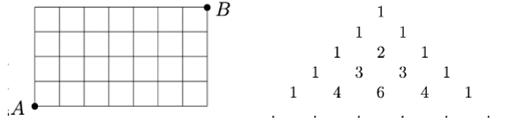
а) Количеству последовательностей из 0 и 1 длины Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} с ровно Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} единицами. б) (Линейный город) Количеству маршрутов путей из Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} в Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} , если идти можно только вправо и вверх (стороны прямоугольника Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n-k} ) в) (Треугольник Паскаля) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -ому числу в Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} -ой строке треугольника Паскаля (нумерация с Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} ) г) (Бином Ньютона) Коэффициенту при мономе Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^kb^{n-k}} в разложении Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a+b)^n} .
- через непосредственное определение - при помощи формулы - используя интерпретации выше Докажите следующие тождества при целых неотрицательныхFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n,k} : а) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n+1}^k = C_{n}^k+C_{n}^{k-1}} б) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n}^k = C_{n}^{n-k}} в) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{2n}^n = (C_{n}^{0})^2+\ldots+(C_{n}^n)^{2}}
Найдите суммы при целых неотрицательных Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n,k,m} : а) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n}^0+ \ldots + C_{n}^n;} б) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n}^0-C_n^1 + \ldots +(-1)^n C_{n}^n;} в) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n}^0+C_n^2 + C_n^4+\ldots} г*) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n}^0+C_n^3 + C_n^6+\ldots} д) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_n^1 + 2 C_n^2 + 3 C_n^3 +\ldots + n C_{n}^n;} е) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n}^0+\frac{1}{2} C_n^1 + \frac{1}{3} C_n^2 + \ldots + \frac{1}{n+1} C_{n}^n;} ж) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{n}^n + C_{n+1}^{n} + \ldots + C_{n+m}^{n};} з) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_n^k+C_{n+1}^{k}+\ldots+C_{n+m}^{k};} и) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_n^k + C_{n+1}^{k+1} + \ldots + C_{n+m}^{k+m};} к) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_n^0C_m^k+ C_n^1C_m^{k-1}+\ldots+C_n^kC_m^0;} л) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (C_n^1)^2 + 2(C_n^2)^2 + 3(C_n^3)^2 + \ldots + n(C_n^n)^2;} м*) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{2n}^{n} + 2C_{2n-1}^{n} + 4C_{2n-2}^{n}+ \ldots + 2^nC_n^{n};} н*) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{2n}^{0} - C_{2n-1}^{1} + C_{2n-2}^{2}+ \ldots + (-1)^nC_n^{n}.}
Найдите Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{(n_1,n_2,n_3), n_1+n_2+n_3=5, n_i \in \N } P(n_1,n_2,n_3) (-1)^{n_1+n_2}} . Посчитайте коэффициенты при Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{57}} и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{57}} в разложении Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x^2 + x^7 + x^9)^{20}} .
В комнате площади Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6} уложены три ковра площади Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3} каждый (форма комнаты и ковров произвольная). Докажите, что какие-то два из этих трёх ковров перекрываются по площади, не меньшей~Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} .
|
| 4 | Рекуррентные соотношения | Для каждого из следующих линейных рекуррентных соотношений найдите общее решение:
а) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+2}- 7a_{n+1}+ 12a_n = 0;} б) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+3} - 2a_{n+2} - 4a_{n+1} + 8a_n = 0} ; в) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+2}+a_{n+1}+a_n=0;} г) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+2}- 9a_n = 0;} д) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+3}+ 3a_{n+2}+ 3a_{n+1} + a_n= 0;} е) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+3}+5a_{n+2}+12a_{n+1}+8a_n=0} .
Найдите решение неоднородного линейного рекуррентного соотношения а) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+2} = a_{n+1} + a_n + 1} ; б) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+2} = 2a_{n+1} - a_n + n + 1} ; в) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+2} = a_{n+1} + 6a_n + 3^n} ?
Числами Фибоначчи называется последовательность Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n,n\geqslant 0} , удовлетворяющая соотношениям Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_0=0} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_1=1} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n=F_{n-1}+F_{n-2}} для всех натуральных Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n>1} .
Найдите формулу для нахождения Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} -ого члена последовательности Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n} .
Найдите
Сколькими способами можно разменять купюру в Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100} рублей на монеты достоинством Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2} и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5} рублей? %364
Найдите рекуррентное соотношение для последовательности Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_n} , где Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_n} -- число способов выложить прямоугольник размера
Сколько существует строк из Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 20} нулей и единиц, в каждой из которых никакие два нуля не стоят рядом?
Докажите, что последовательность с общим членом Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n=n^{k-1}} удовлетворяет соотношению Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n+k} - C_{k}^1 a_{n+k-1} + C_k^2 a_{n+k-2} - \ldots + (-1)^k C_k^ka_n=0} .
В центральной клетке левого столбца доски 1000 × 3 стоит шахматный король. Сколькими спо[1]собами он может добраться до правого столбца доски за 999 ходов? |
| 5 | Разбиения | а) Найдите количество упорядоченных разбиений числа Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
на Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
слагаемых.
б) Найдите общее количество упорядоченных разбиений числа Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} на слагаемые. в) Какой ответ будет в предыдущих пунктах, если мы разрешим слагаемым принимать значение Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} ?
Обозначим через Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(n;n_1,\ldots,n_k)} (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F (n;n_1,\ldots,n_k)} ) количество упорядоченных (соотв. неупорядоченных) разбиений Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} на слагаемые Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_1,\ldots,n_k} .
Справедливы следующие рекуррентные формулы а) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(n;n_1,\ldots,n_k) = f(n-n_1;n_1,\ldots,n_k) + f(n-n_2;n_1,\ldots,n_k) + \ldots + f(n-n_k;n_1,\ldots,n_k)} ; б) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(n;n_1,\ldots,n_k) = F(n-n_1;n_1,\ldots,n_k) + F(n;n_2,\ldots,n_k)} . в) Каковы начальные условия в этих формулах?
а) Что больше: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(20;1,4,6,9)} или Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(20;1,4,6,9)} ? б) Найдите оба числа, используя рекуррентные формулы.
Диаграмма Юнга -- это конечный набор клеток, выровненных по левой границе, в котором длины строк образуют невозрастающую последовательность (каждая строка такой же длины как предыдущая, или короче). Весом диаграммы Юнга называется общее количество клеток диаграммы. Набор чисел, состоящий из длин строк, задаёт разбиение веса диаграммы в сумму слагаемых. Таким образом, есть соответствие между всеми неупорядоченными разбиениями натурального числа Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} и всеми диаграммами Юнга веса Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .
Сколько существует диаграмм Юнга произвольного веса, но имеющих не более Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} строк и не более Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} столбцов?
На доске написано несколько целых положительных чисел: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2} , , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n} . Пишем на другой доске следующие числа: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_0} --- сколько всего чисел на первой доске, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1} --- сколько там чисел, больших единицы, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_2} --- сколько там чисел, больших двойки, и т.~д., пока получаются положительные числа. На этом заканчиваем --- нули не пишем. На третьей доске пишем числа Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_0} , , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_2} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ldots} , построенные по числам второй доски аналогичным образом. Докажите, что наборы чисел на первой и третьей досках совпадают.
|
| 6 | Формальные степенные ряды и производящие функции | Рассмотрим множество последовательностей Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_0,a_1,\ldots,a_n,\ldots)}
(здесь Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_i}
берутся из множества чисел Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Q}
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R}
или ) и введём на них операции сложения и умножения следующим образом:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_0,a_1,\ldots) + (b_0,b_1,\ldots) = (a_0+b_0, a_1+b_1,\ldots);}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_0,a_1,\ldots) \cdot (b_0,b_1,\ldots) = (c_0, c_1,\ldots) \text{, где } c_n = \sum_{j=0}^n a_j\cdot b_{n-j};}
а) Пусть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1= (1,0,0,\ldots,0,\ldots)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = (0,1,0,\ldots,0,\ldots)} .
1) Найдите Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t^2, t^3, \idots, t^n} . 2) Покажите, что любая последовательность Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_0,a_1,\ldots,a_n,\ldots,)} единственным образом представляется в виде Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0 \cdot 1 + a_1 \cdot t + a_2 \cdot t^2 + \ldots + a_n \cdot t^n + \ldots} .
1) Покажите, что все свойства многочленов (коммутативность по сложению/умножению, ассоциативность, дистрибутивность) переносятся на формальные степенные ряды. 2) Пусть дан ряд Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(t)} . Корректна ли операция подстановки вместо Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} ряда Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(t)} ? Ряда Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(t)} без свободного члена?
1) Производная линейна, то есть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\alpha A + \beta B)' = \alpha A' + \beta B'} (здесь Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha,\beta \in \R} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,B} --- формальные степенные ряды). 2) Выполнено тождество Лейбница, то есть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (AB)' = A'B + AB'} . 3) (Ряд Тейлора в нуле). Докажите, что Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n} --- свободный член ряда Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{A^{(n)}}{n!}} .
Найдите коэффициенты ряда $\frac{1}{1-t}$; $\frac1{2-t}$; $\frac1{3+4t}$; $\frac1{(1-t)^{2}}$; $\frac1{(1-t)^{m}}$.
Верно ли равенство $\left(\frac{1}{1-t}\right)^2 \cdot \left(\frac{1}{1+t}\right)^2 = \left(\frac{1}{1-t^2}\right)^2$ для формальных степенных рядов?
Сформулируйте комбинаторное тождество, получаемое при приравнивании коэффициентов в этих рядах.
При каких условиях на степенной ряд Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} его можно разделить на степенной ряд Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} (то есть уравнение Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G\cdot X=F} разрешимо относительно неизвестного степенного ряда Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} )?
При каких условиях на степенной ряд Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} разрешимо уравнение Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^2=F} ?
Пусть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X = \sum_{k=0}^{\infty} \alpha_k t^k} ---- степенной ряд, задаваемый уравнением Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^2 = 1+t} . Найдите коэффициенты Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_0,\alpha_1,\alpha_2,\alpha_3} .
Пусть Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \in \R} . Положим Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\alpha}^n = \frac{\alpha \cdot (\alpha-1) \cdot \ldots \cdot (\alpha-n+1)}{n!}} .
Если Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \in \N, \alpha \geq n} , то Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\alpha}^n} совпадает с биномиальным коэффициентом.
Определим ряд Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1+t)^\alpha = \sum_{n=0}^{\infty} C_{\alpha}^n t^n} . Покажите, что при Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha\in \N} определения согласованы.
Покажите, что Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1+t)^{\alpha} \cdot (1+t)^{\beta} = (1+t)^{\alpha+\beta}} .
Используя определение, найдите коэффициенты ряда Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1+t)^{\frac{1}{2}}}
. Сравните ответ с ответом в задаче предыдущей задаче пункте в.
Вычислите Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=0}^n k^2 C_n^k {(\frac{1}{17})}^k} .
Найдите производящую функцию для числа
Докажите, что функции в последних двух пунктах совпадают.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=0}^{\infty} t^n} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=0}^{\infty} (-1)^n \cdot t^n} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=0}^{\infty} \lambda^n t^n} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{1-t^2}} .
Приведите пример, когда на границе ряда (то есть при Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |t|=R} ) есть сходимость в обеих точках; Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=0}^{\infty}} расходимость в обеих точках; Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=0}^{\infty}} сходимость в одной точке и расходимость в другой точке.
Найдите производящую функцию для последовательности Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n = C_1 \lambda_1^n + C_2 \lambda_2^n} . \pu Какой у неё радиус сходимости?
В каких точках действительной прямой сходится ряд Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum\limits_{n=0}^{\infty}a_nt^n} , где Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n} задано следующим образом? Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n=\begin{cases} 3 \cdot (-6)^n + 4\cdot 3^n, & n=3k, k \in \N; \\ 5 \cdot \left(-\frac{1}{4}\right)^n + 2 \cdot 2^n, & n=3k+1, k \in \N; \\ 6 \cdot (-3)^n, & n=3k+2, k \in \N. \end{cases}}
|
Текущий контроль успеваемости обучающихся по дисциплине:
| № п/п |
Наименование раздела дисциплины |
Форма текущего контроля |
Материалы текущего контроля |
Контрольные вопросы для подготовки к промежуточной аттестации:
| № п/п |
Наименование раздела дисциплины |
Вопросы |
Вопросы/Задания к промежуточной аттестации в устной/письменной форме:
1.
2.
3.
...
48.
49.
50.
...
Перечень учебно-методического обеспечения дисциплины
Список основной литературы:
Список дополнительной литературы:
Методические указания для обучающихся по освоению дисциплины
| Вид учебных занятий/деятельности |
Деятельность обучающегося |
Методы и технологии обучения, способствующие формированию компетенции
| Методы и технологии обучения, способствующие формированию компетенции |