Difference between revisions of "BSc: Introduction to Optimization.F22"
I.konyukhov (talk | contribs) |
Mo.bahrami (talk | contribs) |
||
| (42 intermediate revisions by one other user not shown) | |||
| Line 100: | Line 100: | ||
! Activity Type !! Percentage of the overall course grade |
! Activity Type !! Percentage of the overall course grade |
||
|- |
|- |
||
| − | | Midterm || |
+ | | Midterm || 30 |
|- |
|- |
||
| 2 Intermediate tests || 30 (15 for each) |
| 2 Intermediate tests || 30 (15 for each) |
||
|- |
|- |
||
| − | | Final exam || |
+ | | Final exam || 40 |
| + | |||
| − | |- |
||
| − | | Final presentation || 15 |
||
|} |
|} |
||
| Line 150: | Line 149: | ||
|- |
|- |
||
| Just-in-time teaching || 0 || 0 || 0 |
| Just-in-time teaching || 0 || 0 || 0 |
||
| − | | |
+ | |- |
| Process oriented guided inquiry learning (POGIL) || 0 || 0 || 0 |
| Process oriented guided inquiry learning (POGIL) || 0 || 0 || 0 |
||
|- |
|- |
||
| Line 206: | Line 205: | ||
==== Section 1 ==== |
==== Section 1 ==== |
||
| + | # A steel company must decide how to allocate next week’s time on a rolling mill, which is a machine that takes unfinished slabs of steel as input and can produce either of two semi-finished products: bands and coils. The mill’s two products come off the rolling line at different rates: |
||
| − | {| class="wikitable" |
||
| + | #:: Bands 200 tons/hr |
||
| − | |+ |
||
| + | #:: Coils 140 tons/hr. |
||
| − | |- |
||
| + | #: They also produce different profits: |
||
| − | ! Activity Type !! Content !! Is Graded? |
||
| + | #:: Bands $ 25/ton |
||
| − | |- |
||
| + | #:: Coils $ 30/ton. |
||
| − | | Quiz || 1. What is a product? What are the techniques for describing a product idea in a clear concise manner?<br>2. What user research techniques do you know? In what situations are they applied?<br>3. What are the key customer conversation principles according to the Mom Test technique? Bring an example of bad and good questions to ask.<br>4. What are the 4 phases of the requirements engineering process? <br>5. How do we document requirements? What techniques do you know? || 1 |
||
| + | #: Based on currently booked orders, the following upper bounds are placed on the amount of each product to produce: |
||
| − | |- |
||
| + | #:: Bands 6000 tons |
||
| − | | Presentation || Prepare a short 2-minutes pitch for your project idea (2-5 slides). <br><br>Suggested structure:<br>What problem you are solving:<br>- State the problem clearly in 2-3 short sentences.<br><br>Who are you solving it for:<br>- Who is your user/customer?<br>- Why will they be attracted to it?<br><br>What is your proposed solution to solve that problem:<br>- One sentence description<br>- What main feature(s) will it have? || 0 |
||
| + | #:: Coils 4000 tons. |
||
| − | |- |
||
| + | #: Given that there are 40 hours of production time available this week, the problem is to decide how many tons of bands and how many tons of coils should be produced to yield the greatest profit. Formulate this problem as a linear programming problem. Can you solve this problem by inspection? |
||
| − | | Individual Assignments || A1: Product Ideation and Market Research<br>Formulate 3 project ideas in the following format:<br>X helps Y to do Z – where X is your product’s name, Y is the target user, and Z is what user activity product help with.<br><br>Submit Link to Screenshot board and Feature Analysis Table:<br>- Pick and explore 5 apps similar to your idea<br>- Take screenshots along the way and collect them on a board.<br>- Make a qualitative analysis table for app features.<br><br>Prepare a short 2-minutes pitch for your project idea (2-5 slides). <br><br>Suggested structure:<br>What problem you are solving:<br>- State the problem clearly in 2-3 short sentences.<br><br>Who are you solving it for:<br>- Who is your user/customer?<br>- Why will they be attracted to it?<br><br>What is your proposed solution to solve that problem:<br>- One sentence description<br>- What main feature(s) will it have? || 1 |
||
| + | # Solve the following linear programming problems. |
||
| − | |- |
||
| + | #: maximize <math>6x_1+ 8x_2 + 5x_3 + 9x_4 </math> |
||
| − | | Group Project Work || A2: Forming Teams and Identifying Stakeholders<br>Students are distributed into teams. <br>Meet your team <br>Discuss the idea<br>Agree on the roles<br>Setup task tracker (Trello or similar)<br>Identify 3-5 stakeholders and how to approach them<br>Compose a set of 5 most important questions you would ask from each stakeholder when interviewing them<br><br>Submit<br>A pdf with the idea description, roles distribution among the team, identified stakeholders, ways to approach them, a set of questions for each stakeholder.<br>An invite link to join your task tracker<br><br>A3: Domain Exploration and Requirements<br>User Research Process:<br>Compose the questionnaire for each stakeholder type. <br>Talk to 5-7 stakeholders.<br>Keep updating the questionnaire throughout the process<br>Compose an interview results table<br>Produce personas<br>Summarize most important learning points<br>Describe features your MVP will have (use case diagram + user story mapping)<br><br>Submit a pdf report with:<br>Personas + corresponding questionnaires<br>Interview results table (can provide a link to spreadsheet, make sure to open access)<br>Learning points summary<br>MVP features.<br><br>Optional: <br>Start implementation of the functionality you are certain about.<br><br>Assignment 4. UI design, Prototyping, MVP, and Usability Testing<br>Break down MVP features into phases and cut down the specification to implement MVP V1<br>Produce low and high fidelity designs for your product.<br>Review the phases breakdown.<br>Follow either the Prototyping or MVP path to complete the assignment.<br><br>Prototyping path:<br>Make a clickable prototype with Figma or a similar tool<br>Make 5-10 offline stakeholders use your prototype, observe them and gather feedback<br>Embed your prototype into an online usability testing tool (e.g. Maze).<br>Run an online usability test with 5-10 online stakeholders.<br>Summarize key learning points<br><br>MVP path:<br>Review your MVP phases.<br>Build MVP V1 <br>Make 5-10 offline stakeholders use your MVP, observe them and gather feedback<br>Integrate an online usability testing tool to observe user sessions (e.g. Smartlook).<br>Distribute the MVP to 5-10 online stakeholders and run an online usability test.<br>Summarize key learning points<br><br><br>Submit all of the below in one PDF:<br>Link to sketches and designs.<br>Link to your MVP/Clickable prototype.<br>Link to online usability test.<br>Names of people you conducted the tests with and which stakeholder type are they.<br>Key learning points summary.<br><br>Make sure all links are accessible/viewable. || 1 |
||
| + | #: subject to <math>2x_1+ x_2 + x_3 + 3x_4 \leq 5 </math> |
||
| − | |} |
||
| + | #:: <math>x_1 + 3x_2 + x_3 + 2x_4 \leq 3 </math> |
||
| + | #:: <math>x1, x2, x3, x4 \geq 0 </math> |
||
| + | # Give an example showing that the variable that becomes basic in one iteration of the simplex method can become nonbasic in the next iteration. |
||
| + | # Solve the given linear program using the dual–primal two phase algorithm. |
||
| + | #: maximize <math>2x_1 - 6x_2</math> |
||
| + | #: subject to <math>-x_1 - x_2 - x_3 \leq -2</math> |
||
| + | #:: <math>2x_1 - x_2 + x_3 \leq 1 </math> |
||
| + | #:: <math>x1, x2, x3 \geq 0 </math> |
||
| + | |||
==== Section 2 ==== |
==== Section 2 ==== |
||
| + | # Find the minimum of the function <math> f = \lambda / log \lambda </math> using the following methods: |
||
| − | {| class="wikitable" |
||
| + | #* Newton method |
||
| − | |+ |
||
| + | #* Quasi-Newton method |
||
| − | |- |
||
| + | #* Quadratic interpolation method |
||
| − | ! Activity Type !! Content !! Is Graded? |
||
| + | # State possible convergence criteria that can be used in direct search methods. |
||
| − | |- |
||
| + | # Why is the steepest descent method not efficient in practice, although the directions used are the best directions? |
||
| − | | Quiz || 1. What does the acronym MVP stand for? What types of MVP do you know of?<br>2. Define roles, activities, and artefacts of Scrum. What differentiates Scrum from other Agile frameworks, e.g. Kanban?<br>3. What does DEEP criteria stand for when discussing Product Backlog? Explain each of the aspects with examples.<br>4. Describe how Scrum activities are performed. Which of them are essential and which of them can vary depending on the product. || 1 |
||
| + | # What is the difference between quadratic and cubic interpolation methods? |
||
| − | |- |
||
| + | # Why is refitting necessary in interpolation methods? |
||
| − | | Presentation || Prepare a 5-mins presentation describing your: <br>product backlog<br>sprint results<br>MVP-launch plan<br>Each team will present at the class. The assessment will be based on the presentation delivery, reasoning for decision making and asking questions and providing suggestions for other teams. || 0 |
||
| + | # What is a direct root method? |
||
| − | |- |
||
| + | # What is the basis of the interval halving method? |
||
| − | | Group Project Work || Assignment 5. Developing an MVP<br>1. Populate and groom product backlog: <br>Comply with the DEEP criteria. <br>2. Run two one-week sprints:<br>Conduct two Sprint plannings, i.e. pick the tasks for Sprint Backlog.<br>Conduct two Sprint reviews<br>Run one Sprint Retrospective<br>3. Make a launch plan and release:<br>You need to launch in the following two weeks.<br>Decide what functionality will go into the release.<br>Release your first version in Google Play.<br>Hint: Focus on a small set of features solving a specific problem for a specific user, i.e. MVP.<br>4. Prepare a 5-mins presentation describing your: <br>product backlog<br>sprint results<br>MVP-launch plan.<br>Demo for your launched MVP.<br>Each team will present at the class. The assessment will be based on the presentation delivery, reasoning for decision making and asking questions and providing suggestions for other teams.<br>5. Submit a PDF with:<br>Backlogs and Launch plan<br>Link to the launched product<br>Assignment 6. Launch your product, AC and DoD.<br>1. Improve the UX: Getting Started with the App.<br>2. Release in Google Play: Work on packaging it nicely<br>3. Design and deploy a landing page<br><br>4. Produce acceptance criteria for 3-5 most important user stories in your product.<br>5. Produce definition of done checklist<br>6. Estimate the items in your product backlog<br><br> || 1 |
||
| + | # What is the difference between Newton and quasi-Newton methods? |
||
| − | |- |
||
| + | |||
| − | | Group presentation || Midterm Presentation<br>1. Prepare a midterm presentation for 10-mins in which you cover:<br>The problem you are trying to solve<br>Your users and customers (personas)<br>Your solution and it's core value proposition<br>Current state of your product<br>Clear plan for the upcoming weeks<br>Your team and distribution of responsibilities<br>Demo<br>Retrospective and learning points<br>Link to your app<br><br>Submit a pdf with:<br>Items 1, 2, 3<br>link to the presentation<br> || 0 |
||
| − | |} |
||
==== Section 3 ==== |
==== Section 3 ==== |
||
| + | # Solve the following LP problem by dynamic programming: |
||
| − | {| class="wikitable" |
||
| + | #: Maximize <math> f (x_1, x_2) = 10x_1 + 8x_2</math> |
||
| − | |+ |
||
| + | #: subject to <math> 2x_1 + x_2 \leq 25</math> |
||
| + | #:: <math> 3x_1 + 2x_2 \leq 45</math> |
||
| + | #:: <math> x_2 \leq 10 </math> |
||
| + | #:: <math> x1, x2 \geq 0</math> |
||
| + | #: Verify your solution by solving it graphically. |
||
| + | # Consider the following tree solution for a minimum cost network flow problem: |
||
| + | #:[[Image:ItO_p1.png]] |
||
| + | #:As usual, bold arcs represent arcs on the spanning tree, numbers next to the bold arcs are primal flows, numbers next to non-bold arcs are dual slacks, and numbers next to nodes are dual variables. |
||
| + | #* For what values of is this tree solution optimal? |
||
| + | #* What are the entering and leaving arcs? |
||
| + | #* After one pivot, what is the new tree solution? |
||
| + | #* For what values of is the new tree solution optimal? |
||
| + | |||
| + | === Final assessment === |
||
| + | ==== Section 1 ==== |
||
| + | # Solve the following linear programming problems. |
||
| + | #: maximize <math>x_1 + 3x_2</math> |
||
| + | #: subject to <math>-x_1 - x_2 \leq -3</math> |
||
| + | #:: <math>-x_1 + x_2 \leq -1</math> |
||
| + | #:: <math>-x_1 + 2x_2 \leq 2</math> |
||
| + | #:: <math>x1, x2 \geq 0</math> |
||
| + | # Give an example showing that the variable that becomes basic in one iteration of the simplex method can become nonbasic in the next iteration. |
||
| + | # Solve the given linear program using the dual–primal two phase algorithm. |
||
| + | #: maximize <math>6x_1 + 8x_2 + 5x_3 + 9x_4</math> |
||
| + | #: subject to <math>x_1 + x_2 + x_3 + x_4 = 1</math> |
||
| + | #:: <math>x_1, x_2, x_3, x_4 \geq 0</math> |
||
| + | ==== Section 2 ==== |
||
| + | # Perform two iterations of the steepest descent method to minimize the function given from the stated starting point <math>(-1.2, 1)</math> |
||
| + | #:: <math>f(x_1, x_2) = 100(x_2 - x_1^2 )^2 + (1 - x_1)^2</math> |
||
| + | # Minimize <math>f = 2x_1^2 + x_2^2</math> by using the steepest descent method with the starting point <math>(1, 2)</math> (two iterations only). |
||
| + | # Minimize <math>f = x_1^2 + 3x_2^2 + 6x_3^2</math> by Newton's method using the starting point as <math>(2,-1, 1)</math> . |
||
| + | ==== Section 3 ==== |
||
| + | * It is proposed to build thermal stations at three different sites. The total budget available is 3 units (1 unit = $10 million) and the feasible levels of investment on any thermal station are 0, 1, 2, or 3 units. The electric power obtainable (return function) for different investments is given below. Find the investment policy for maximizing the total electric power generated. |
||
| + | {| class="wikitable" style="height:14em;" |
||
|- |
|- |
||
| + | ! Return function Ri(x) !! i = 1 !! i = 2 !! i = 3 |
||
| − | ! Activity Type !! Content !! Is Graded? |
||
|- |
|- |
||
| + | | R0(x) || 0 || 0 || 0 |
||
| − | | Quiz || 1. What are common product hypotheses present? How can we formulate them as questions about our UX?<br>2. Explain what is hypothesis-driven development<br>3. Describe the important aspects and elements of a controlled experiment || 1 |
||
| + | |- |
||
| + | | R1(x) || 2 || 1 || 3 |
||
|- |
|- |
||
| + | | R2(x) || 4 || 5 || 5 |
||
| − | | Presentation || Prepare a short 2-minutes pitch for your project idea (2-5 slides). <br><br>Suggested structure:<br>What problem you are solving:<br>- State the problem clearly in 2-3 short sentences.<br><br>Who are you solving it for:<br>- Who is your user/customer?<br>- Why will they be attracted to it?<br><br>What is your proposed solution to solve that problem:<br>- One sentence description<br>- What main feature(s) will it have? || 0 |
||
|- |
|- |
||
| + | | R3(x) || 6 || 6 || 6 |
||
| − | | Group project work || Assignment 7: Development, Observation, and Product Events.<br>1. Continue with your development process:<br>- Hold sprint planning and reviews.<br>- Revisit estimations and keep track for velocity calculation.<br>- Host demos and release new versions to your users<br><br>2. Observing users:<br>- Integrate a user sessions recording tool into your product<br>- As a team: watch 100 user sessions and outline common user behavior patterns.<br>- Each team member: give product to 3 new people and observe them use it.<br><br>3. Product events:<br>Create a product events table.<br>Integrate a free analytics tool that supports events reporting (e.g. Amplitude, MixPanel).<br><br>Write and submit a report:<br>- describe user behavior patterns (main ways how people use your product).<br>- learning points from the observations<br>- add the events table.<br>- describe which analytics tool you chose and why<br><br>Assignment 8: GQM, Metrics, and Hypothesis-testing.<br>1. GQM and Metrics Dashboard<br>- Compose a GQM for your product.<br>- Identify your focus and L1 metrics<br>- Setup an Analytics Dashboard with the metrics you chose.<br>- Add the instructors to your Analytics Dashboard.<br><br>Hypothesis-testing:<br>- answer clarity and hypotheses: do users understand your product, is it easy for them to get started, and do they return?<br>- suggest product improvements to increase clarity, ease of starting and retention.<br>- based on the suggestions formulate 3 falsifiable hypotheses<br>- design a simple test to check each of them<br>- pick one test that could be conducted by observing your users<br>- conduct the test<br><br>Submit:<br>- GQM, Focus and L1 Metrics breakdown.<br>- Report on the hypothesis-testing activities<br>- Access link to the dashboard.<br>Assignment 9: Running an A/B test<br>Compose an A/B test:<br>- Design a change in your product<br>- Hypothesis: Clearly state what you expect to improve as the result of the change.<br>- Parameter and Variants: Describe both A and B variants (and other if you have more).<br>- Intended sample size.<br>- OEC: Determine the target metric to run the experiment against.<br><br>Then do one of the two options:<br>Option 1: Conduct the A/B test using a remote control and A/B testing tool (Firebase, Optimizely or like)<br><br>Option 2: Do the statistical math yourself<br>Conduct an A/B test and collect data.<br>Do the math manually using the standard Student T-test.<br><br>Submit a PDF with:<br>- the A/B test description <br>- report on how the experiment went.<br>- either screenshots from the tool or math calculations. || 1 |
||
|} |
|} |
||
| + | * A fertilizer company needs to supply 50 tons of fertilizer at the end of the first month, 70 tons at the end of the second month, and 90 tons at the end of the third month. The cost of producing x tons of fertilizer in any month is given by $<math>(4500x + 20x^2)</math>. It can produce more fertilizer in any month and supply it in the next month. However, there is an inventory carrying cost of $400 per ton per month. Find the optimal level of production in each of the three periods and the total cost involved by solving it as an initial value problem. |
||
| − | === Final assessment === |
||
| + | * Consider the following tree solution for a minimum cost network flow problem: |
||
| − | '''Section 1''' |
||
| + | *: [[Image:ItO_p2.png]] |
||
| − | # Grading criteria for the final project presentation: |
||
| + | *: As usual, bold arcs represent arcs on the spanning tree, numbers next to the bold arcs are primal flows, numbers next to non-bold arcs are dual slacks, and numbers next to nodes are dual variables. |
||
| − | # Problem: short clear statement on what you are solving, and why it’s important. |
||
| + | *:: For what values of is this tree solution optimal? |
||
| − | # User: should be a specific user, can start from generic and then show how you narrowed it. |
||
| + | *:: What are the entering and leaving arcs? |
||
| − | # Solution: how do you target the problem, what were the initial assumptions/hypotheses |
||
| + | *:: After one pivot, what is the new tree solution? |
||
| − | # Elicitation process: interviews, how many people, what questions you asked, what you learnt. |
||
| + | *:: For what values of is the new tree solution optimal? |
||
| − | '''Section 2''' |
||
| − | # Arriving at MVP: how you chose features, describe prototyping and learning from it, when did you launch, and how it went. |
||
| − | # Team and development process: how it evolved, what were the challenges, what fixes you made to keep progressing. |
||
| − | # Product demo: make it clear what your current product progress is. |
||
| − | '''Section 3''' |
||
| − | # Hypothesis-driven development: how did you verify value and understandability of your product, what were the main hypotheses you had to check through MVP. |
||
| − | # Measuring product: what metrics you chose, why, what funnels did you set for yourself, and what was the baseline for your MVP. |
||
| − | # Experimentation: What usability tests and experiments you conducted, what did you learn, how did it affect your funnels and metrics. |
||
=== The retake exam === |
=== The retake exam === |
||
| + | Retakes will be run as a comprehensive exam, where the student will be assessed the acquired knowledge coming from the textbooks, the lectures, the labs, and the additional required reading material, as supplied by the instructor. During such comprehensive oral/written the student could be asked to solve exercises and to explain theoretical and practical aspects of the course. |
||
| − | '''Section 1''' |
||
| − | # Grading criteria for the final project presentation: |
||
| − | # Problem: short clear statement on what you are solving, and why it’s important. |
||
| − | # User: should be a specific user, can start from generic and then show how you narrowed it. |
||
| − | # Solution: how do you target the problem, what were the initial assumptions/hypotheses |
||
| − | # Elicitation process: interviews, how many people, what questions you asked, what you learnt. |
||
| − | '''Section 2''' |
||
| − | # Arriving at MVP: how you chose features, describe prototyping and learning from it, when did you launch, and how it went. |
||
| − | # Team and development process: how it evolved, what were the challenges, what fixes you made to keep progressing. |
||
| − | # Product demo: make it clear what your current product progress is. |
||
| − | '''Section 3''' |
||
| − | # Hypothesis-driven development: how did you verify value and understandability of your product, what were the main hypotheses you had to check through MVP. |
||
| − | # Measuring product: what metrics you chose, why, what funnels did you set for yourself, and what was the baseline for your MVP. |
||
Latest revision as of 17:30, 1 September 2022
Introduction to Optimization
- Course name: Introduction to Optimization
- Code discipline: CSE???
- Subject area: Data Science and Artificial Intelligence
Short Description
The course outlines the classification and mathematical foundations of optimization methods, and presents algorithms for solving linear and nonlinear optimization. The purpose of the course is to introduce students to methods of linear and convex optimization and their application in solving problems of linear, network, integer, and nonlinear optimization. Course starts with linear programming and moving on to more complex problems. primal and dual simplex methods, network flow algorithms, branch and bound, interior point methods, Newton and quasi-Newton methods, and heuristic methods. Current states, literature, techniques, theories, and methodologies are presented and discussed during the semester.
Prerequisites
Prerequisite subjects
- CSE201: Mathematical Analysis I
- CSE202: Analytical Geometry and Linear Algebra I
- CSE203: Mathematical Analysis II
- CSE204: Analytical Geometry and Linear Algebra II
Prerequisite topics
- Basic programming skills.
- OOP, and software design.
Course Topics
| Section | Topics within the section |
|---|---|
| Linear programming |
|
| Nonlinear programming |
|
| Extensions |
|
Intended Learning Outcomes (ILOs)
What is the main purpose of this course?
The main purpose of this course is to enable a student to go from an idea to implementation of different optimization algorithms to solve problems in different fields of studies like machine and deep learning, etc.
ILOs defined at three levels
We specify the intended learning outcomes at three levels: conceptual knowledge, practical skills, and comprehensive skills.
Level 1: What concepts should a student know/remember/explain?
By the end of the course, the students should be able to ...
- remember the different classifications and mathematical foundations of optimization methods
- remember basic properties of the corresponding mathematical objects
- remember the fundamental concepts, laws, and methods of linear and convex optimization
- distinguish between different types of optimization methods
Level 2: What basic practical skills should a student be able to perform?
By the end of the course, the students should be able to ...
- Funderstand the basic concepts of optimization problems
- evaluate the correctness of problem statements
- explain which algorithm is suitable for solving problems
- evaluate the correctness of results
Level 3: What complex comprehensive skills should a student be able to apply in real-life scenarios?
By the end of the course, the students should be able to ...
- understand the basic foundations behind optimization problems.
- classify optimization problems.
- choose a proper algorithm to solve optimization problems.
- validate algorithms that students choose to solve optimization problems.
Grading
Course grading range
| Grade | Range | Description of performance |
|---|---|---|
| A. Excellent | 90-100 | - |
| B. Good | 75-89 | - |
| C. Satisfactory | 60-74 | - |
| D. Fail | 0-59 | - |
Course activities and grading breakdown
| Activity Type | Percentage of the overall course grade |
|---|---|
| Midterm | 30 |
| 2 Intermediate tests | 30 (15 for each) |
| Final exam | 40 |
Recommendations for students on how to succeed in the course
- Participation is important. Attending lectures is the key to success in this course.
- Review lecture materials before classes to do well.
- Reading the recommended literature is optional, and will give you a deeper understanding of the material.
Resources, literature and reference materials
Open access resources
- Convex Optimization – Boyd and Vandenberghe. Cambridge University Press.
Closed access resources
- Engineering Optimization: Theory and Practice, by Singiresu S. Rao, John Wiley and Sons.
- Bertsimas, Dimitris, and John Tsitsiklis. Introduction to Linear Optimization. Belmont, MA: Athena Scientific, 1997. ISBN: 9781886529199.
Software and tools used within the course
- MATLAB
- Python
- Excel
Activities and Teaching Methods
| Teaching Techniques | Section 1 | Section 2 | Section 3 |
|---|---|---|---|
| Problem-based learning (students learn by solving open-ended problems without a strictly-defined solution) | 0 | 0 | 0 |
| Project-based learning (students work on a project) | 1 | 1 | 1 |
| Modular learning (facilitated self-study) | 0 | 0 | 0 |
| Differentiated learning (provide tasks and activities at several levels of difficulty to fit students needs and level) | 1 | 1 | 1 |
| Contextual learning (activities and tasks are connected to the real world to make it easier for students to relate to them) | 0 | 0 | 0 |
| Business game (learn by playing a game that incorporates the principles of the material covered within the course) | 0 | 0 | 0 |
| Inquiry-based learning | 0 | 0 | 0 |
| Just-in-time teaching | 0 | 0 | 0 |
| Process oriented guided inquiry learning (POGIL) | 0 | 0 | 0 |
| Studio-based learning | 0 | 0 | 0 |
| Universal design for learning | 0 | 0 | 0 |
| Task-based learning | 0 | 0 | 0 |
| Learning Activities | Section 1 | Section 2 | Section 3 |
|---|---|---|---|
| Lectures | 1 | 1 | 1 |
| Interactive Lectures | 1 | 1 | 1 |
| Lab exercises | 1 | 1 | 1 |
| Experiments | 0 | 0 | 0 |
| Modeling | 0 | 0 | 0 |
| Cases studies | 0 | 0 | 0 |
| Development of individual parts of software product code | 0 | 0 | 0 |
| Individual Projects | 1 | 1 | 1 |
| Group projects | 0 | 0 | 0 |
| Flipped classroom | 0 | 0 | 0 |
| Quizzes (written or computer based) | 0 | 0 | 0 |
| Peer Review | 0 | 0 | 0 |
| Discussions | 1 | 1 | 1 |
| Presentations by students | 1 | 1 | 1 |
| Written reports | 0 | 0 | 0 |
| Simulations and role-plays | 0 | 0 | 0 |
| Essays | 0 | 0 | 0 |
| Oral Reports | 0 | 0 | 0 |
Formative Assessment and Course Activities
Ongoing performance assessment
Section 1
- A steel company must decide how to allocate next week’s time on a rolling mill, which is a machine that takes unfinished slabs of steel as input and can produce either of two semi-finished products: bands and coils. The mill’s two products come off the rolling line at different rates:
- Bands 200 tons/hr
- Coils 140 tons/hr.
- They also produce different profits:
- Bands $ 25/ton
- Coils $ 30/ton.
- Based on currently booked orders, the following upper bounds are placed on the amount of each product to produce:
- Bands 6000 tons
- Coils 4000 tons.
- Given that there are 40 hours of production time available this week, the problem is to decide how many tons of bands and how many tons of coils should be produced to yield the greatest profit. Formulate this problem as a linear programming problem. Can you solve this problem by inspection?
- Solve the following linear programming problems.
- maximize
- subject to
- Give an example showing that the variable that becomes basic in one iteration of the simplex method can become nonbasic in the next iteration.
- Solve the given linear program using the dual–primal two phase algorithm.
- maximize
- subject to
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x1, x2, x3 \geq 0 }
Section 2
- Find the minimum of the function using the following methods:
- Newton method
- Quasi-Newton method
- Quadratic interpolation method
- State possible convergence criteria that can be used in direct search methods.
- Why is the steepest descent method not efficient in practice, although the directions used are the best directions?
- What is the difference between quadratic and cubic interpolation methods?
- Why is refitting necessary in interpolation methods?
- What is a direct root method?
- What is the basis of the interval halving method?
- What is the difference between Newton and quasi-Newton methods?
Section 3
- Solve the following LP problem by dynamic programming:
- Maximize
- subject to
- Verify your solution by solving it graphically.
- Consider the following tree solution for a minimum cost network flow problem:
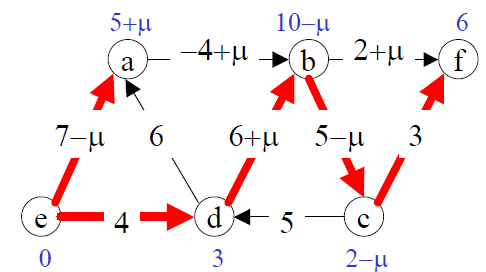
- As usual, bold arcs represent arcs on the spanning tree, numbers next to the bold arcs are primal flows, numbers next to non-bold arcs are dual slacks, and numbers next to nodes are dual variables.
- For what values of is this tree solution optimal?
- What are the entering and leaving arcs?
- After one pivot, what is the new tree solution?
- For what values of is the new tree solution optimal?
Final assessment
Section 1
- Solve the following linear programming problems.
- maximize
- subject to
- Give an example showing that the variable that becomes basic in one iteration of the simplex method can become nonbasic in the next iteration.
- Solve the given linear program using the dual–primal two phase algorithm.
- maximize
- subject to
Section 2
- Perform two iterations of the steepest descent method to minimize the function given from the stated starting point
- Minimize by using the steepest descent method with the starting point (two iterations only).
- Minimize by Newton's method using the starting point as .
Section 3
- It is proposed to build thermal stations at three different sites. The total budget available is 3 units (1 unit = $10 million) and the feasible levels of investment on any thermal station are 0, 1, 2, or 3 units. The electric power obtainable (return function) for different investments is given below. Find the investment policy for maximizing the total electric power generated.
| Return function Ri(x) | i = 1 | i = 2 | i = 3 |
|---|---|---|---|
| R0(x) | 0 | 0 | 0 |
| R1(x) | 2 | 1 | 3 |
| R2(x) | 4 | 5 | 5 |
| R3(x) | 6 | 6 | 6 |
- A fertilizer company needs to supply 50 tons of fertilizer at the end of the first month, 70 tons at the end of the second month, and 90 tons at the end of the third month. The cost of producing x tons of fertilizer in any month is given by $. It can produce more fertilizer in any month and supply it in the next month. However, there is an inventory carrying cost of $400 per ton per month. Find the optimal level of production in each of the three periods and the total cost involved by solving it as an initial value problem.
- Consider the following tree solution for a minimum cost network flow problem:
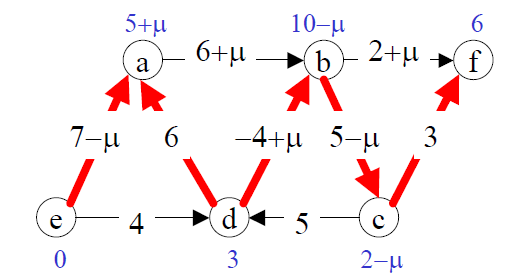
- As usual, bold arcs represent arcs on the spanning tree, numbers next to the bold arcs are primal flows, numbers next to non-bold arcs are dual slacks, and numbers next to nodes are dual variables.
- For what values of is this tree solution optimal?
- What are the entering and leaving arcs?
- After one pivot, what is the new tree solution?
- For what values of is the new tree solution optimal?
The retake exam
Retakes will be run as a comprehensive exam, where the student will be assessed the acquired knowledge coming from the textbooks, the lectures, the labs, and the additional required reading material, as supplied by the instructor. During such comprehensive oral/written the student could be asked to solve exercises and to explain theoretical and practical aspects of the course.

























